内積とは何でしょうか。高校では a・b=|a||b|cosθ で2本のベクトルの内積を定義します(θは2本のベクトルのなす角。ここではベクトルを高校流の矢印付きの文字でなく、太字で表しています)。テキストにはそう書いてあるだけですから、先生も「これを内積と言います」と説明するでしょう。ここで多くの生徒は「内積って一体、何?」と思うのではないでしょうか。大学では内積が満たすべき性質をいくつかあげ、「これらの性質を満たす、ベクトル2本をスカラーに対応させる写像を内積と呼ぶ」などと説明したりします。そして「ベクトル空間で内積を定義すると、ベクトルの長さ、なす角を考えることができるようになります」と続きます。そうか、じゃあ役に立つね、と何となく納得しますし、まあそれでもよいのです。というよりそれが数学な気もします。しかしここで話題にしたいのはそういうことではなく、もっと身にしみる(?)説明です。
物理や工学をやっている人ならすぐ答えられるでしょう。「仕事」です。仕事とは……おもりをF(kg重)の力でr(m)引っ張ったとき、「おもりはFr(kg重・m)の仕事をされた」と言います。今、斜めに引っ張ることを考えましょう。おもりは、床の上を水平方向にしか動かないものとしておきます。

Fの有効な成分(水平方向の成分)は|F|cosθですから、rだけ変位(位置が変わる)する間にされた仕事Wは、W=(|F|cosθ)×|r|=|F||r|cosθ となります。これ、F・rですよね。物理学的には、F・rは仕事なのです。
なお、上の図みたいに、Fが一定で大きさで一定の角度で引っ張る、なんてケースでは「仕事なのです」と言ったって「ああそうですか」で終わりそうですが、曲がった曲線Cに沿ってFも場所によって変化する場合でも仕事は
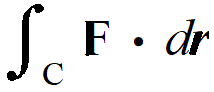
で計算することができるのでした。「曲線Cに沿って線積分する」と言います。こうなると「内積ってありがたい!」となりそうです。