
としましょう。これはいつもよく使っている直交座標(いつものx、y座標)と極座標(原点からの距離をr、x軸から左回りに測った角がθ)の間の変換の式なのでした。偏導関数を求めておきます。

今、ベクトル2本を次のように定義します。
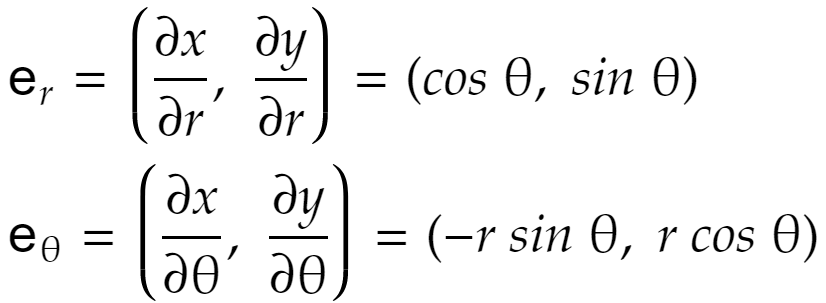
これはそれぞれr軸、θ軸方向のベクトルです。そして、成分はx、y系で測った値です。……★
一般化します。次のように(x, y)座標系と(u, v)座標系があるとしましょう。もちろん、図のように直交座標などの仮定はありません。
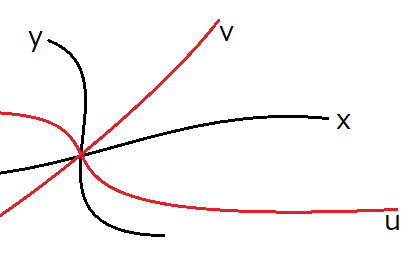
2本のベクトルを次で定義します。もちろん必要な微分可能性は満たされているという前提です。

このとき、この2本のベクトルはそれぞれx軸方向、y軸方向のベクトルです。そして、成分は u, v 系で測った値です。
……と書かれて、読んだ人はみんなすぐ理解できるんでしょうか……。ぼくは★を見て、「なぜ??」と思いました。一般化した方の主張の成立の理由を説明しましょう。
x軸に沿ってΔx(≒0)だけ移動したとするとu成分、v成分の変化はそれぞれ

です。そして、Δx≒0 のときは下の図で水色の四角形は平行四辺形だと考えられます。

従ってx軸方向の変位は

と考えられます。これはaがx軸方向のベクトルであり、u, v 成分を使って表せば(Δu, Δv)であることを示しています。もちろん Δu, Δv は u, v 軸で測った値です。
なおここではx軸に沿った原点からの変位を考えましたが、yを任意に固定して得られる平面上の曲線(方程式はy=c)上の変位について考えても同じです。
このa,bは曲線座標系の各点での基底となります。『テンソル』(石原繁1991裳華房)ではこれを自然基底と呼んでいます。
とうとう1都3県に緊急事態宣言がでるかも。去年の2月頃はまさかこんな風になるなんて思いもしなかった……。イヤだ、イヤだでは始まりませんからなるべくこの機会を前向きに捉えたいですが、それにしても大変な災難です……。