物理を勉強中です。とりあえず力学をしっかりやって、解析力学、量子力学と進めるつもりでいます。
数学はもちろんたくさん出てきます。しかし、仕方がないのですが、「これ、いいのかな?」という議論が少なくありません。それなりの説明で一応納得しておきたいので、他人に説明できるレベルを自分のハードルにして、解決したら忘れないようにメモしています。今回の記事はそのうちのひとつです。
平面上の各点でベクトルが決まっています。ベクトル場が定義されている、ということです。空間でもよいのですが大して変わらないので平面で話を進めます。例えば平面上の各点で力 F が定まっている、といった状況を考えます。このとき、F = f(x, y) = f(p) です。このとき dp が微小なベクトルであるとして、平面上の曲線Cに沿ってf(x, y)・dp の総和を考えます。これが接線線積分です。記号では
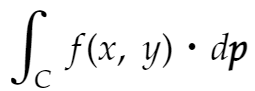
と書きます。物体が点(x, y)で受ける力がf(x, y) であるとき、上の式は物体が曲線Cに沿って移動するときにされる仕事を意味するのでした。特にfが勾配であったとき、つまり∇fであったとき、接線線積分は簡単に計算できます。fの勾配とは
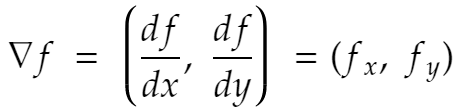
のことです。
よく見かける説明は
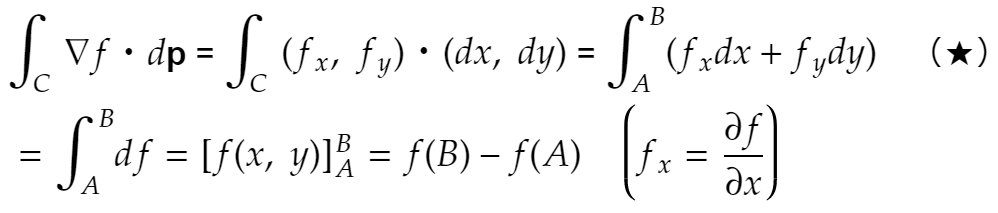
というものです。曲線Cは点Aから始まり点Bで終わる、としています。つまり勾配の接線線積分の値は、曲線が途中でどうなっていても関係ありません。始点と終点で決まってしまうのです。何となくでいいなら正しそうです。★の部分を見てください。積分記号の後ろは「全微分」というやつで、だから上のような式変形が可能なのです。
最初「ナルホド!」と思ったのですが、よく考えると何だかおかしい。積分の計算で点を代入、っていいのかな、これ。正しそうではあるけれど。……と思ったら次のような説明もあります。
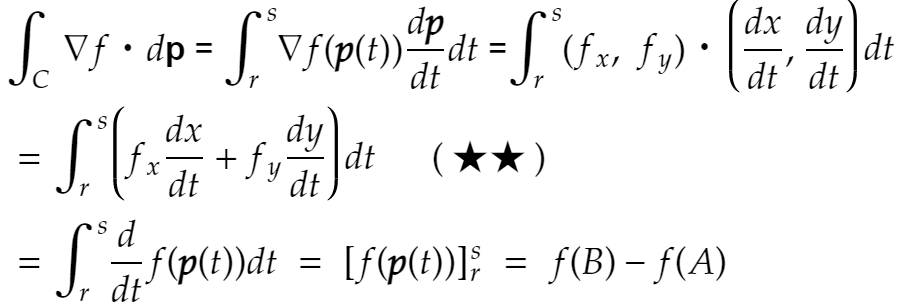
これなら隙がない。★★からの変形は、多変数の合成関数の微分法を(逆に)使っているだけなので、文句のつけようがありません。
とりあえずあまり厳密に、厳密に、……とはやらないでとにかく計算をできるように、と考えています。そうした上で余裕があれば細かな点を考えればいいでしょう。コリオリの力の辺りも見直してみました。面白いです。大学生の頃もっと勉強しておけばいろいろ変わったかも知れません。高校の物理はすごく面白くて、数学より成績もずっとよかったです。でも議論の雑な部分が気になっていたことも確かです。多少は気にせず勉強してみます。