前、同僚だった先生に聞かれました。下の図で、直線EFはGHと平行です。点Aが直線EF上を動くとき、角θが最大になるのはAG=AHのときであることを示してください。
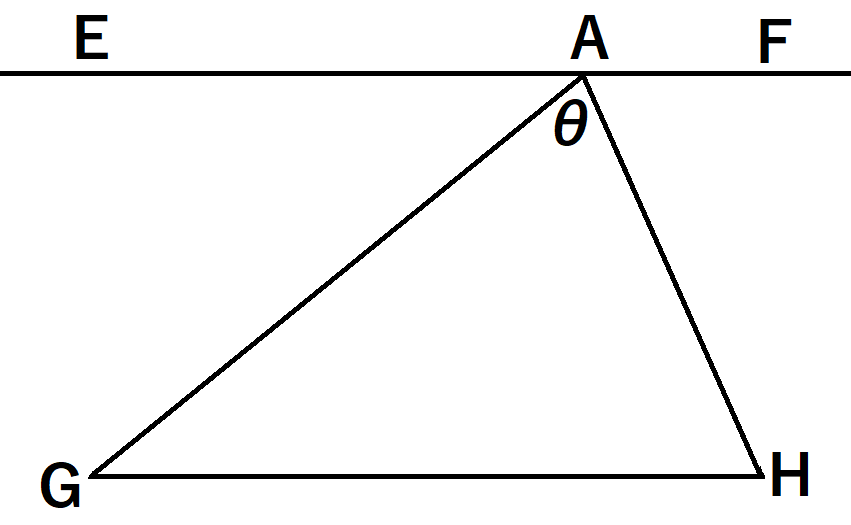
センター試験か共通テストの問題を解くのに、これが必要だったそうです。証明ではなく、この事実が。
幾何の問題だから幾何学的に解けた方がいいかも……と思ってあれこれ考えましたがうまくいきません。仕方なく座標軸を持ち出しました。上下左右に拡大縮小すればいいので、下の図のように考えればいいでしょう。xは点Aのx座標です。xがいろいろに変わったとき、角θがいつ最大になるか調べればよいですね。
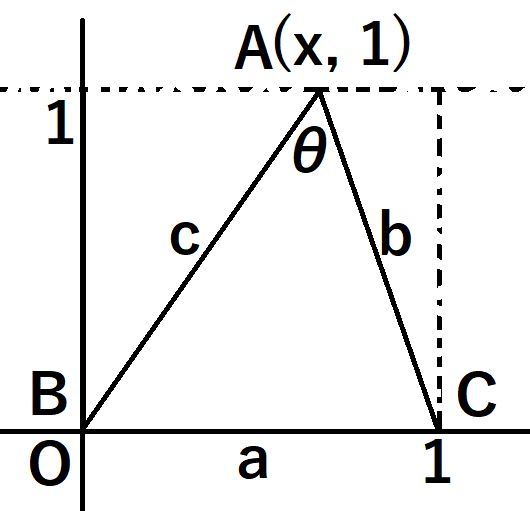
次が成立します。
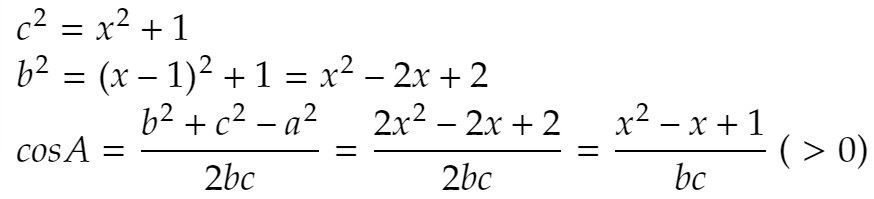
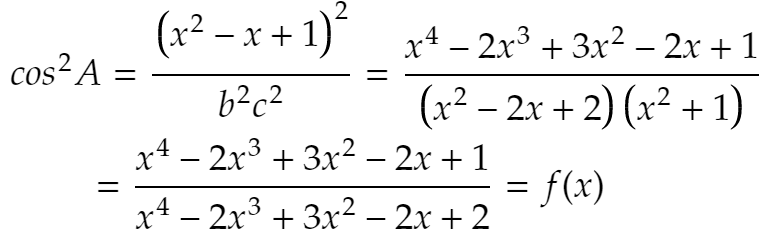
とおくと、

導関数の符号の変化を調べて確かに最大になることを示せば完璧です。
一応これで終わりですが意外でした。現象自体は明らかで、簡単に示せそうな問題なのに、こんな方法しか思いつきません。計算も楽ではないし、他にないのかな……という感じです。気づかないだけかも知れません。誰か教えてください!
追記 2021年3月12日(金)
cos A =……の式で、判別式は負ですから cos A > 0。よって2乗して比較してもよろしい。だから f(x) が最大になるときを調べればよいわけです。