3元連立1次方程式を解きます。行列で次のように書きましょう。
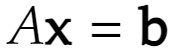
成分で書いておきます。成分の添え字は行を上付き、列を下付きで書きます。前々回の続きです。
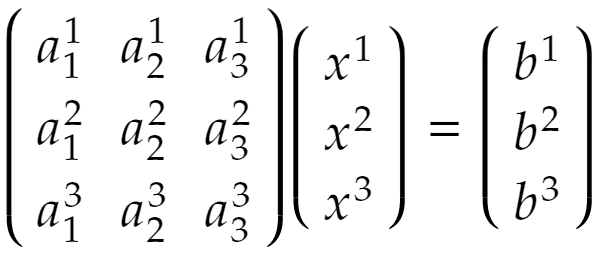
あるいは
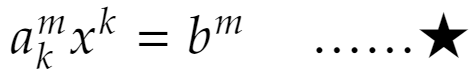
とも書けるのでした。アインシュタインの規約を使っています。これはm行目の成分の等式です。凄まじい便利さですね!!
Aは逆行列を持つとし、
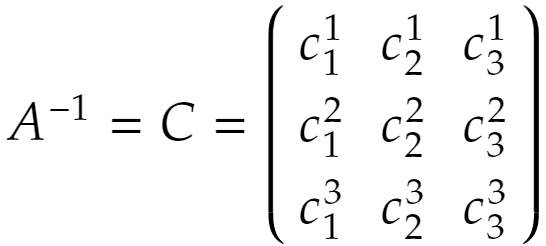
であるとします。解を行列を使って書くなら
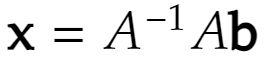
とやり、成分で書きたいなら成分を代入すればいいだけです。ここでは★から直に解を求めてみます。
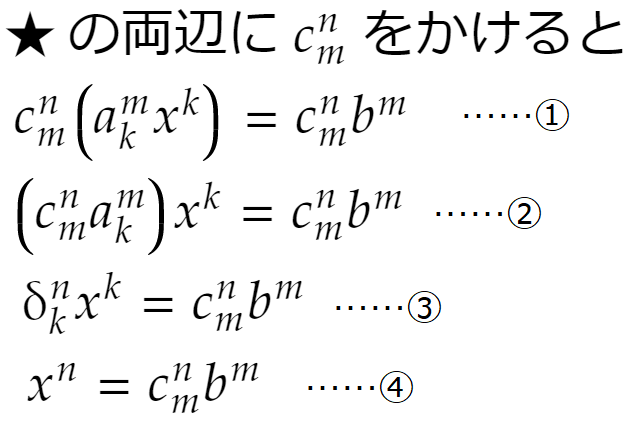
②から③はよいでしょうか。CはAの逆行列なので、前々回(「アインシュタインの規約とは何か」)の解説に従って変形しました。
では③から④までは? 3次の行列の話だとすると
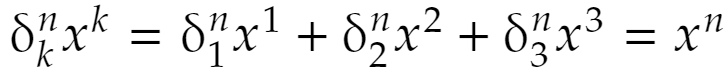
です。1≦n≦3で、値は不明ですがクロネッカーのδの性質により、

だから上のような式が成立するのです。
①から②まではどうでしょうか。いや、そもそもその前に
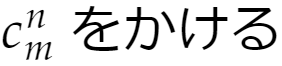
とはどういうことでしょうか。これ自体は単なる数ですが、アインシュタインの規約を使うつもりでかけているのです。だから①から②までの結合法則っぽいものが成立するのかとか、怪しそうです。しかし次のように考えれば成立することが分かります。
そもそも、

と書けるのでした。だから、怪しいと思ったらこの式に戻ればよいですね。
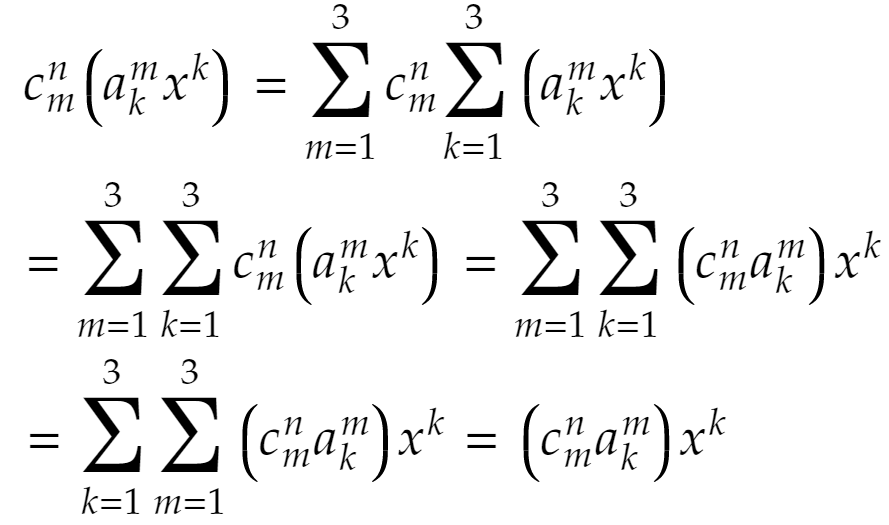
かけ算っぽく見えますが、実際にはアインシュタインの規約を考えているわけでかけ算でありません。しかし、ここで示したように、単純にかけてもよいことが分かりました!
Σを使うと面倒くさい……という精神的なストッパーがかかりそうですが、アインシュタインの規約を使えば気持ちが楽です。
ここからテンソル解析につながります。勢いづいたところで頑張ってみます。