前、偶順列、奇順列の話を書きました。
上の記事を見て偶順列、奇順列の復習をしておいてください。行列式を定義するのに使います。
奇順列をー1に、偶順列を1に対応させる関数εを考えます。εの値を順列の符号と呼びましょう。ε(偶順列)=1、ε(奇順列)=-1です。例えば
ε(123456)=1、ε(213456)=-1
となります。従って
ε(123456)=ーε(213456)
が成立です。どんな順列も1回の数字の入れ換えで奇順列は偶順列に、偶順列は奇順列に変わるのでした。あとで使うので次の問題を見ておきます。
-------------------------
ijk、pqrは1,2,3の順列だとします。何回かの文字の入れ替えでijkは123に、同じ入れ替えで123はpqrに変わったとして、ε(pqr)とε(ijk)の間に成り立つ関係を調べてください。
-------------------------
n回の入れ換えで
ijk → 123
と変わり、同じ入れ換えで
123 → pqr
と変わったとすると
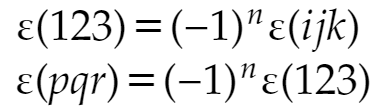
が成立します。1回の入れ換えで順列の符号が反転するからです。この2式からε(123)を消去すれば
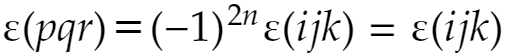
従って
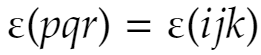
が成立します。意外と言うか、ちょっと面白い気がします。
次回、このεを使って行列式を定義します。テキストでよく見かけるのは置換群を用いた方法ですが、大学1年生、数学科であってもまだ代数を勉強していなかったり、あるいは物理や化学を専攻している学生などは置換による定義は意味が分かりづらいはずです。順列の符号を使った方法は分かりやすいと言えます。