こんなのをべき級数というのでした。

これはeのx乗をマクローリン展開したものです。収束など細かなことを言わず形式的にこの式を導くだけなら高校3年の知識があれば十分です。元気な先生は「こんなのが成立する!」と教えているかも知れません。もちろんこれが正しいのかどうかは問題です。無限級数なのでそもそも収束しないかも知れませんし、特定の範囲のxに対してだけ収束するのかも知れません。また、収束したとしても本当に左辺に一致するかどうか分かりません。高校数学の範囲で無理するとしたら、

とおいて両辺をxで繰り返して微分することになると思います。荒技ですよね。無限項ある級数を微分するのですから。でも、そういった気になる点はあるにしても、数学が好きな生徒なら「おおっ!」と思うのではないでしょうか。夢があります。
このべき級数ですが、今後少し使いそうなので周辺の定理や事実、場合によっては証明を何回かに分けてまとめておこうと思います。
ーーーーーーーーーーーーーーーーーーーー

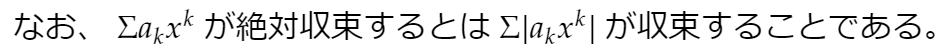

ーーーーーーーーーーーーーーーーーーーー
とりあえずこれだけ分かっていれば最初の級数は任意のxに対して収束することが分かります(何に収束するかはこれだけでは分かりませんが)。確認してみると
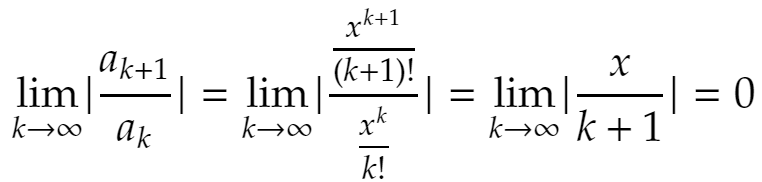
ですから、上の載せた事実によれば収束半径rはr=+∞。つまりどんなxに対しても収束です。これで胸を張って「収束です!」と言えますね! 証明はこの事実だけなら大変ではありません。大学生向けの微積分のテキストに書いてあります。公式集風にパッと見てすぐ定理などが分かるよう(特に自分が……)、ブログにまとめます。
Pythonのコードなど、自分で載せたものを結構使っています。やはり、情報は使いやすい形で一カ所にまとめておくと役に立つのです。あちこちにバラバラ、「あれはどこだっけ?」となるとストレスです。