平面スカラー場を f(x, y) とします。つまり平面の各点に数値 f(x, y) が対応している、ということです。何のことはない、要するに z = f(x, y) という空間内の曲面があり、平面上の各点で高さ z が決まっていると思えばよいのです。実用では z は温度であったり、密度であったり、いろいろです。ここで、曲線 C : f(x, y) = K (Kは定数)を考えましょう。これは地図で言う等高線です。xy平面上の曲線 C では高さ K だということです。
さて、∇(ナブラ)という記号があります。例えば
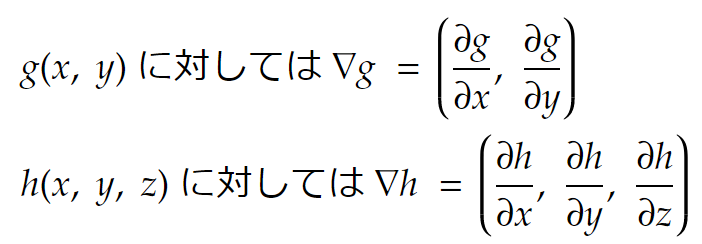
です。この∇hを「hの勾配」と言います。また、∇hの代わりに grad h とも書きます。つまり∇h= grad h です。
さっきのfに対して∇fを考えましょう。これは図形的に何を意味しているのでしょうか。等高線を x = x(t), y = y(t) と表しておきます。このとき f(x(t), y(t)) = K の両辺を t で微分して、
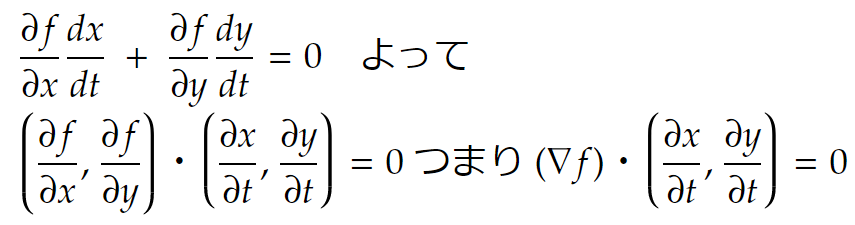
を得ます。この式で
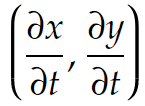
は曲線 C 上の(x, y)での接線ベクトルです。つまり、∇fは等高線と垂直なのです。数学では等高線でなく等位線と言います。また空間の話では等位面と呼び、∇h(x, y, z)は空間内の曲面h(x, y, z) = K (等位面)と垂直になります。
この事実を使う例を挙げましょう。
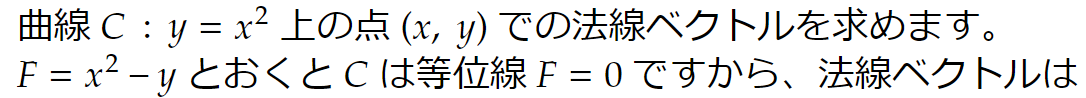
∇F = [2x, -1] となります。例えば (3, 9) での法線ベクトルは [6, -1] となるわけです。
もうひとつ。平面 D : 3x+4y+2z=6 の法線ベクトルを求めましょう。
F = 3x + 4y + 2z - 6 とおけば、F = 0 は等位面(Fが一定の値、0である曲面)ですから、∇F=[3, 4, 2] は法線ベクトルです。世代によっては高校で「平面 ax + by + cz = d の法線ベクトルは [a, b, c]である」という事実を習っていると思います。
ここのところ、ベクトル解析を頑張って復習中です。ストークスの定理も終わり。以前に紹介したマセマの『ベクトル解析 キャンパス・ゼミ』は説明が丁寧で分かりやすいと思います。
が、ストークスの定理の証明に一部納得できないところがあります。賢い人が見ればよいのかも知れませんが、ぼくは『物理入門コース 物理のための数学』で理解しました。こちらも素晴らしい本で、前にも紹介しました。
いわゆる「物理数学」の本です。線積分、多重積分、発散定理、ストークスの定理などについて1章あてられており、短いページですが極めて効率よく分かりやすく解説されています。マセマの本で演習まで済ませてからこの本を読みました。頭の中が整理された感じです。
勉強中にテキストを変えると定義や定理の順番などが変わってしまい、よくない面もありますが、同じ定理を色々な角度から見ることができるというメリットもあります。
追記:
空間でも∇Fは等位曲面と垂直になる、と書きました。その理由を説明しておきます。等位曲面上の点Pを通る任意の曲線Cを考えましょう。平面の時と同じく、C上の点Pでの接線ベクトルは∇Fと垂直です。Cは任意ですから∇Fはその点での法線ベクトルとなるのです。

