だいぶ前、こんな記事を書きました。
↑ うまくいっていません。その後ときどきあれこれ考えていたんですが、いいこと思いついた!! これならどうだ!?
「正項級数は、どう並べ替えても、その上でどこにどう括弧をつけても(括弧は有限個でも無限個でもよく、カッコ内の項数は有限個でも無限個でもよい)和は変わらない」を示します。なお、(単に)並べ替えた級数の和は一致することは事実として使います。また隣り合う何項かを括弧で括っても和は変わらないという事実も使います(微積分のテキストにはちゃんとした証明が載っています)。
問題を見やすくしましょう。正項級数から項を自由に選んで和をつくり、括弧をつけて
(…………)+(…………)+(…………)+……………… (★)
という和を考えてみます。もちろん1回選んだ項はもう選べませんし、選ばない項があってはなりません。また括弧内は無限項でも有限項でも構いませんし、括弧は無限個でも構いません。こうしたとき、この和はもとの和と一致するのでしょうか。元の数列は収束し、和をSとしておきます。
最初の括弧の内容を表の1段目、次の括弧を2段目、……と下の表のように数列の項を配置します。有限項しか入っていない括弧があれば0を補います。横の和を yi とすると、これは収束します。元の数列を適切に入れ換えれば(和Sは変わらない)、その数列のある部分列が横1行分の数列になります。正項級数ではこの数列の和はS以下です(すぐ示せます)。従って収束です。
★の和を計算することは、下の表で
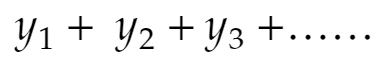
を求めることです。

青字に注目してください。ジクザグに加えた和を
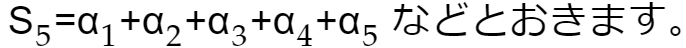
このとき、

要するに、関わりのある項を含む横の列の和は加えるわけです。一般に次が成立するような△が見つかります。

n→∞ とすれば

が分かります。
一方、次が成立します。

理屈は同じなので小さな例で説明しましょう。次が成立することを示します。

Sを作る項を次のように並べ替えます(考え方を示すための例です。何をしているのか、数行後に分かりますから一瞬、我慢してください)。

収束する正項級数なので、一部を括弧で括っても収束し、しかも和は変わりませんから次が言えます。

ここで

は仮定から収束ですが、これは次の数列のある部分列の和になっています。

従って

が言えます。なお、ここでも先ほどと同様に、正項級数では部分列の和は元の級数の和以下になることを使いました。
(2)でn→∞ とすれば

となります。
(1)、(3)より次が言えます。これで終わりです。

多分、間違いなさそうだと思うんですが……。しかし、こういう話、全然見かけません。「和が収束する正項数列は順序をどう変えても和は変わらない」というのは本に載っているのです。しかし今回取り上げたような主張は見たことがありません。みんな、当たり前だと思っているから問題にしないのでしょうか。あるいは考え方によっては明らかで、今回のこの記事はただ大げさに書いているからなのか。
ま、どっちでももう構いません。とりあえず事実が分かったので満足です。