無限級数の和についてひとつ、話しましょう。まず次の定理を証明します。

考えてみれば、何となくでよいなら当たり前です。数列がαに収束するということは、nが大きければどの項もまあほぼ α と思ってよいということ。もうほとんどαばっかりです。だからそれらの平均を取るとαに近づくでしょう。しかしこれでは証明になりません。ちゃんとやります。
もとの数列がαに収束するとは、与えられたεに対してNが存在して
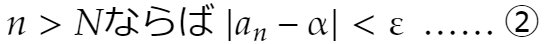
が成立することです。
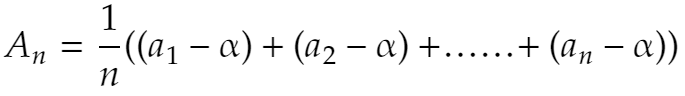
とおきます。
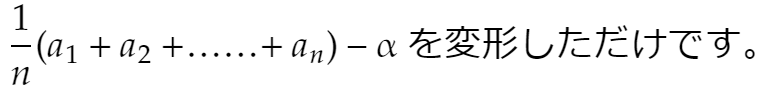
これが②の仮定の下でいくらでも小さくできることを示せばよいですね。
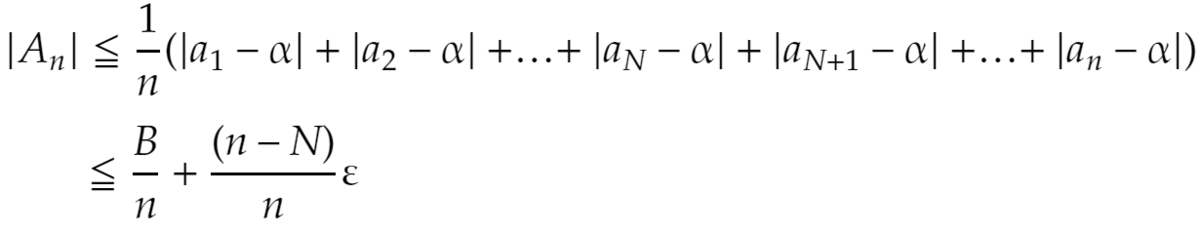
なお、
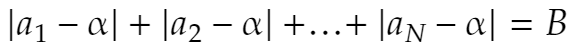
とおきました。これは与えられた ε で決まる定数です。これで証明できました。nを十分大きく取れば
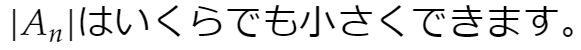
(任意に 2ε>0 を与えます。εに対し②を満たすNが見つかります。BはNで定まる定数なので
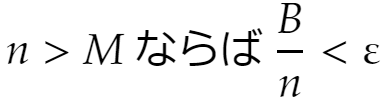
となるMが存在します。また、
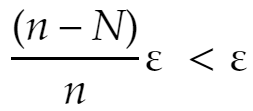
はつねに成立です。
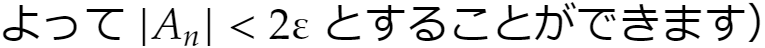
さて、チェザロの和というのがあります。通常、数学では
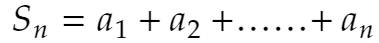
とおいてn→∞としたときの極限値で数列の無限和を定義します。これが普通な気はしますが、そうしなければいけないと決まっているわけでもありません。実際、チェザロの和で無限和を定義してもよいのです。チェザロの和とは、
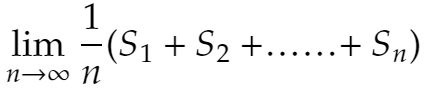
が収束するときの極限値を言います。これがSに収束するとき、

の総和はSである、と定義するのです。チェザロの和が存在すれば、もとの数列は「チェザロの意味で総和可能」と言われます。最初に示した定理によれば
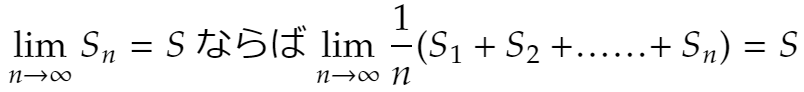
ですから、通常の和が収束するならチェザロの意味でも総和可能で、チェザロの和と一致します。
チェザロの和があっても通常の和はないことがあります。数列
1,-1,1,-1,……
では通常の和はありません。しかし、

なのですから
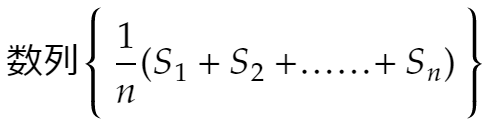
は 1,1/2,2/3,2/4,3/5,3/6,…… です。偶数項目の一般項はn/(2n-1)ですから極限値は1/2。結局全体の極限値、つまりチェザロの和は1/2です。通常の和は、存在すればチェザロの和に一致するが、チェザロの和が存在したからと言って通常の和が存在するとは限らないのです。
2020年8月5日(水)
一部修正しました。