行列式について少し書きました。
今回は転置行列の行列式を考えます。行列Aの行列式の定義は次でした。
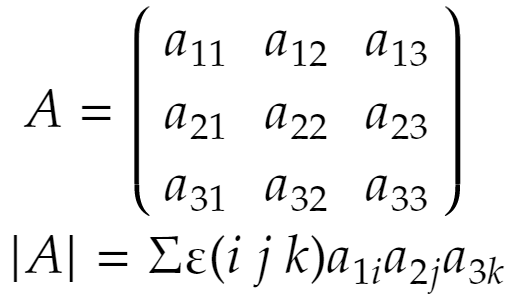
転置行列とはもとの行列の行と列を入れ換えた行列です。
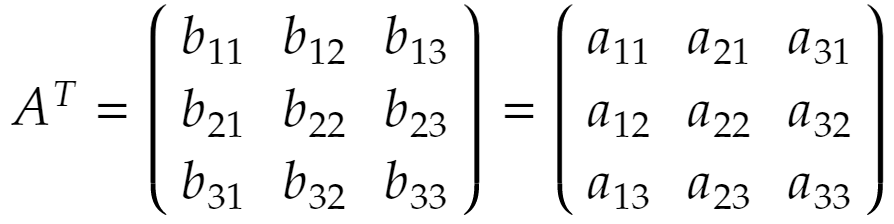
この転置行列の行列式は
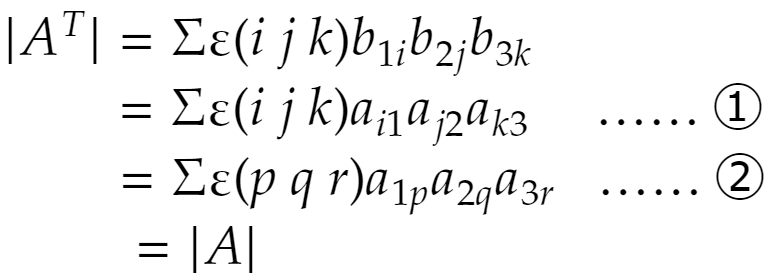
となって、もとの行列式に一致するのです。①から②までを説明しましょう。①は行列式の定義の式に合いません。Σ以降の部分は、行が1、2、3と変化しなければならないのでした。だから

としたいのです。もちろん i, j, k は1,2,3の並べ替えです。このとき
ε(i, j, k) = ε(p, q, r) が成立するのでした。次の記事に書いてあります。
だから

が成立するのです。なかなか面白い証明だなー、と思いました。
この機会に線形代数、ベクトル解析を復習しておこうと思って次の本を読んでいます。非常によくまとまっている印象。工学系の学生に向けた本だと思いますが、 証明はキッチリしています。証明を省いているところもうやむやにせず、そう書いてあります。
なお、今回の証明はこの本に書いてあったのではありません。次の本です。

