空間内に平行四辺形ABCDがあります。座標を見ると分かりますが、直線ABは平面y=y0(zx平面と平行)上にあり、直線ADは平面x=x0(yz平面と平行)上にあります。ここでm1は直線ABのzx平面内での傾き、m2は直線ADのyz平面内での傾きです。
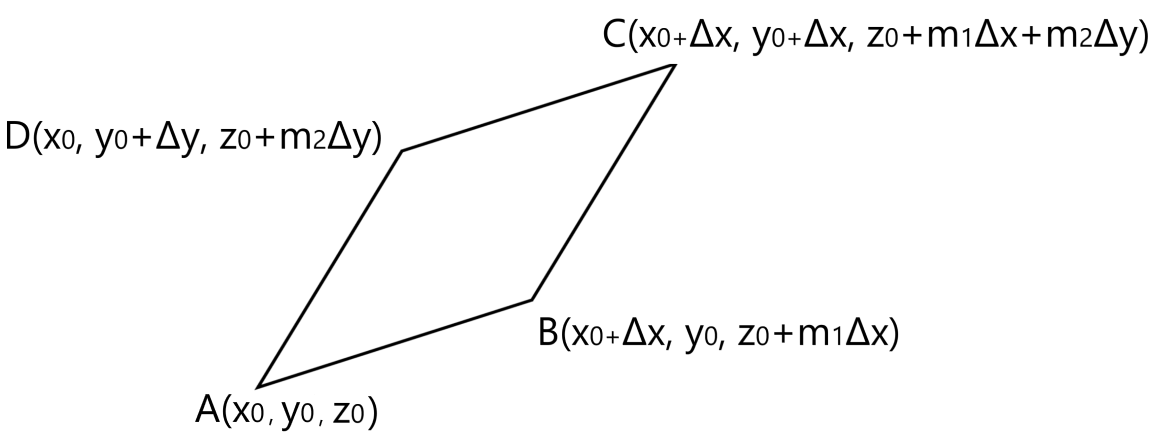
点Cの座標が(x0+Δx, y0+Δy, z0+m1Δx+m2Δy)であることは、AB間のzの増分がDC間のzの増分と等しい(四角形ABCDは平行四辺形なのでした)ことから分かります。
前回の記事ではA(x0, y0, z0)を通る平面で、zx平面との交線の傾きがm1、yz平面との交線の傾きがm2であるものの式を求めました。次のようになるのでした。
z-z0=m1(xーx0)+m2(y-y0)
もしも、関数 z = f(x, y) で fx(x0, y0) , fy(x0, y0) (偏微分係数)が存在すれば、ここまでの議論からAでの接平面の候補の式は
z-z0=fx(x0, y0)(xーx0)+fy(x0, y0)(y-y0)
となることが分かります。なぜ「接平面」でなく「接平面の候補」なのかと言うと……、x軸方向、y軸方向を考えたときに偏微分係数が存在したとしても、その他の方向では滑らかになっていない可能性があるからです。つまり、曲面をx軸方向、y軸方向にスーッと滑らかに移動できたとしても、x軸とy軸の間の方向(直線y=xに沿う方向など)では点Aから先がスコン!と切れ落ちてしまっているかも知れないのです。その場合、「接平面」と呼ぶわけにはいきません。
どんな方向からAに近づいてもそんなことが起こらないようにするための条件、つまりAで接平面が存在するための条件が「全微分可能」です。関数
z = f(x, y) が(x0, y0)で全微分可能とは、
f(x0+Δx, y0+Δy) =f(x0, y0)+ fx(x0, y0)Δx+fy(x0, y0)Δy+ε
とおくとき、Δx,Δy→0 ならば
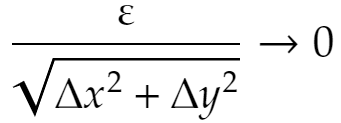
となることです。Δx,Δyは0に近づくこと以外に値に制限はなく、もちろん負でもよく、従ってこの条件が満たされれば曲面上でAにどんな近づき方をしても「滑らかである」ということになります。すると、次が言えます。
z = f(x, y) が(x0, y0)で全微分可能であるとき、曲面 z = f(x, y) の、A(x0, y0, z0) における接平面は
z-z0=fx(x0, y0)(xーx0)+fy(x0, y0)(y-y0)
である。
また、以下も分かります。
関数が(x0, y0)で全微分可能なら、Δx,Δyの絶対値が小さければ
f(x0+Δx, y0+Δy) ≒f(x0, y0)+ fx(x0, y0)Δx+fy(x0, y0)Δy
と近似できる。
何となくでいいなら「大抵成立しているよな~」、という感じですが、そうでない例はいくらでもあります。
次は「全微分」です!! 物理でも出てきます。