例を用います。平面の極座標を考えましょう。
x = r cos θ、y = r sin θ
というものでした。偏導関数を求めておきます。
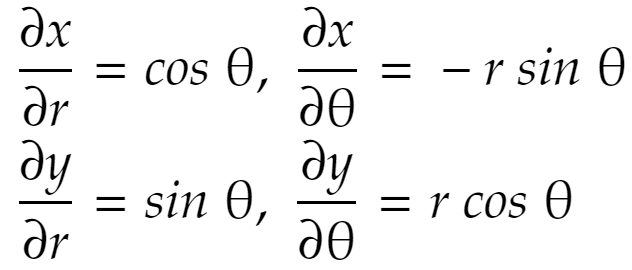
これらを成分に持つ、次のようなベクトルを考えます。

これは後で使います。
平面上でごく近い2点間の距離を求めます。
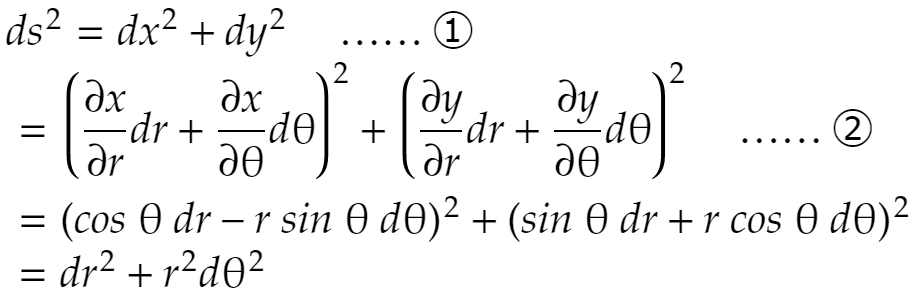
①から②までは全微分の式を使っています。 全微分についてはこれ ↓。
極座標でdr, dθだけ動いた点までの距離がこう書けるのです。
先ほど求めた、


このベクトルを使うと、実は次の式が成立することが分かっています。

実際、それぞれの内積を計算してみれば
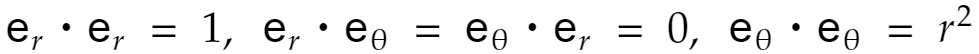
ですから、確かに上の式が正しいことは分かります。ここで内積を次のように置きます。
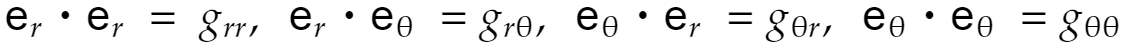
するとさっきの式は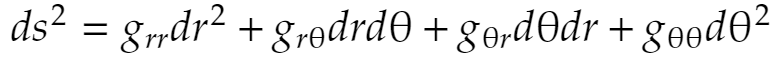
となります。
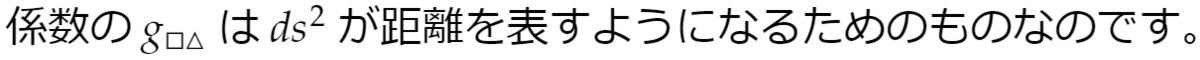
この係数は計量テンソルと呼ばれます。
別の機会にまた詳しく書いてみます。アインシュタインの一般相対性理論にはテンソルがたくさん出てきます。テンソルを自在に使えるようでないと本を読むことすらできません。努力あるのみです。