ブログの内容に関する問い合わせをいただきました。次の記事に誤りがあるとのことでした。
見てみると、面積を求める式として体積を求める式を書いているなど間違いが。ご指摘、ありがとうございます。次の通り訂正します。
-------------------
半径rの円の面積をで微分すると円周の長さになります。球の体積をrで微分すると球の表面積になります。生徒に話すと一様に「えっ!?」と驚いてくれるところです。どうしてこうなるのか、説明しましょう。


図で、半径に沿ってr~r+Δrの部分の同心円を考えます。幅 Δrのドーナツ型です。この部分の面積は近似的に
![]()
です。従って、量の求め方の原理によれば半径Rの円の面積Sは次の式で与えられます。
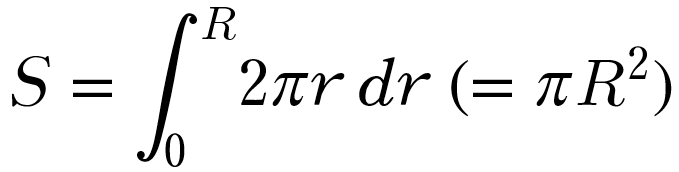
これが理由なのです。「円周を積分すると面積になる」ということが分かると思います。
体積の方も同様です。球をタマネギみたいに考え、幅Δrの薄皮を積分すると全体が求まる、という式から分かります。

こうして量の求め方の原理、微小量Δxを使って議論するって面白いです。いろいろなことがどんどん分かる。微分方程式を立てるときにも微小量を考えたりします。
------------------------------
もとの記事も一応残し、最初にこの記事へのリンクを追加しておきました。お気づきの点があればお教えいただけると助かります。