次の和をべき級数というのでした。このべき級数の収束半径について少し書いておきます。べき級数に対し -r < x < r の範囲で収束、|x| > r では発散というrがあり、これを収束半径と言います。なお、x=±rのときの収束発散は級数によっていろいろです。

まず、上のべき級数と次の②は収束半径が一致します。

それは②が収束する場合、②は

のように書き換えられるからです(級数は収束する場合、定数を括り出せる)。③のカッコ内が収束するか否かで②がどうなるかも決まり、だから収束半径も一致するのです。
次に、①は級数
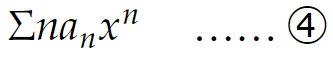
とも収束半径が一致します(n=0,1,2,……)。①、④はかなり(?)違った級数で、もちろん収束先は変わるにしても収束半径が一致するというのはいかにも不思議に思えます。これを示しましょう。
①の収束半径をr、④の収束半径をr’とします。
(1)|x| < r ’ のとき

べき級数は収束半径内なら絶対収束ですから(定理)、

は収束、よって上の不等式から

も収束です。よって①も収束です。
(2)|x| < r のとき
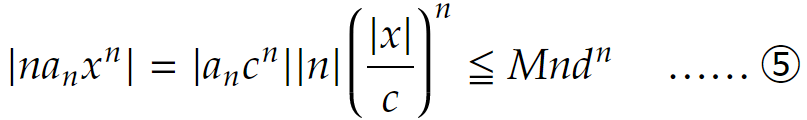

となります。c は①の収束半径内の値ですから、

は収束、よって

は有界なのです。ここで⑤の一番右の辺について、

が成立しますから、ダランベールの判定法により

は収束します。従って

が収束、よって

は収束です。これより r ≦ r ' が言えました。
以上(1)、(2)から r = r ' となります。つまり①、④の収束半径は一致するのです。
実は級数

も収束半径が同じになります。(2)でnの代わりにn+1を使うだけで示せます。
今回示した事実は、べき級数の項別微分、項別積分の証明に使えます。『級数』(井上、勝俣、林1998共立出版)にあります。
この本は実数列(や実数値関数の列)に限って級数の基本的な定理、性質などをまとめたものです。簡単な練習問題付き。見やすく「まとめ」みたいなのをつけて欲しい気もしますが、証明は分かりやすく、便利に使っています。100ページとコンパクトなので持ち歩きやすいです。目次は次の通り。
第1章 数列,連続関数
1.1 上限と下限
1.2 数列の極限の基本性質
1.3 いろいろな数列の極限
1.4 数列の収束条件
1.5 関数の極限
1.6 連続関数
1.7 補足
第2章 級数
2.1 級数の収束と基本性質
2.2 正項級数
2.3 絶対収束と収束条件
2.4 補足
第3章 関数項級数
3.1 関数列
3.2 関数項級数
3.3 整級数
3.4 関数の整級数展開
3.5 Fourier級数
3.6 補足
問題の略解とヒント
索引
あまり級数に特化した本は見かけませんし、読んでいて楽しい本だと思います。関数列の一様収束、もちろん項別微分や項別積分、最後にはフーリエ級数にも触れています。複素数列でも実数列と収束の証明などは大して変わらないので、そちらにも役立つと思います。
