半径1の円の内部に点(x,y)があります。u=x+y、v=xyとおくとき、点(u,v)の存在する範囲を求めましょう。
よくある問題ですが、うーん、どうもイマイチ不安な解答を見かけます。
(x,y)は原点中心、半径1の円の内部にあるので
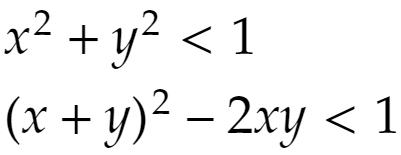
が成立します。よって
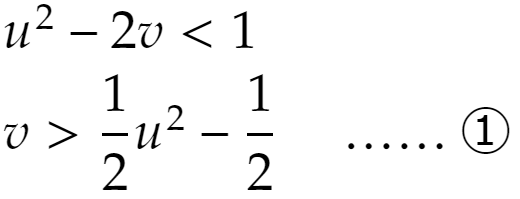
u=x+y,v=xyなのでx、yは2次方程式
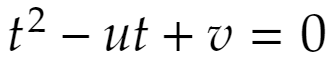
の解です。x、yは実数ですから判別式をDとして
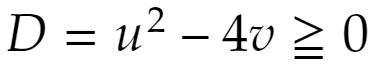
が成立しなければなりません。つまり
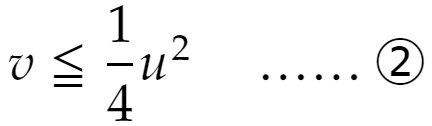
が成立しなければなりません。以上から答えは①かつ②の領域、となります。文字はuをxに、vをyに書き換えればいいでしょう(どの文字を使うかは本質的ではありません)。
まあいいと言えばいいんでしょうが……もう少し明確にするならこう考えましょう。
例えば(1,2)は問題の存在範囲に入っているのでしょうか。つまりu=1,v=2になることはあるのでしょうか。この点は①を満たしますがまだ心配なことがあります。1=x+y,2=xyが成立するような実数x,yが存在しなければなりません。このx,yは
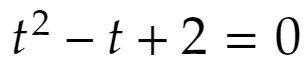
の2解ですから、判別式D≧0となればOKです。しかしこの場合
D=1-4・1・2<0ですから、実数x,yはありません。よって(1,2)は答えには含まれません。
……と、こんなことが分かっているなら最初のような解答を書いてもよいかも知れません。分かっていなくて、答えの作り方だけを憶えているならまずいと思います。
同じような心配のある問題について前、書きました。
見比べてみて下さい。