次の不等式を示しましょう。
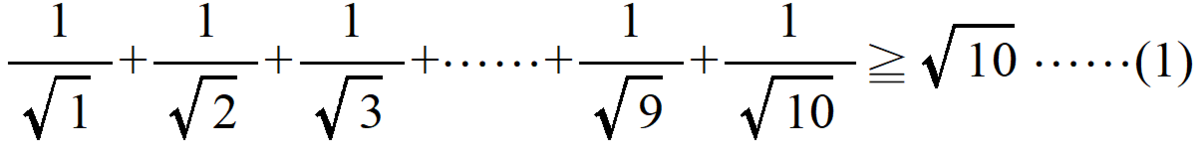
ただし、なぜか
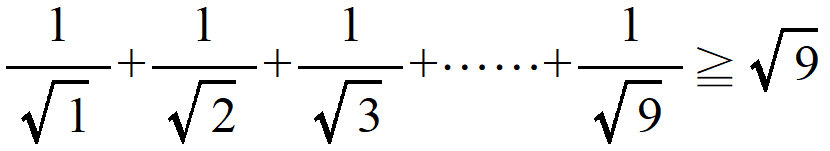
であることは分かっているとします。この式の両辺に1/√10 を加えると

が得られます。ここで、もしも
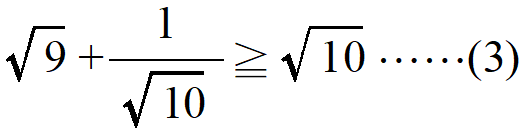
を証明できれば、(2)と(3)を組み合わせて
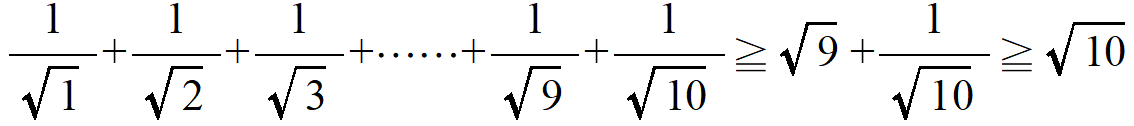
となりますから、一番左の辺と一番右の辺を見て(1)が言えますね。(3)を示すなら電卓とかでもいいですし、(3)の両辺を2乗した
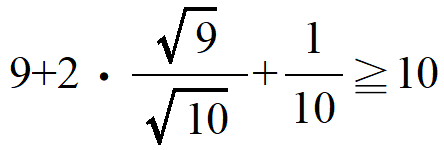
を示してもいいでしょう。これは、式変形してみれば
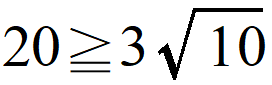
と同値ですから、成り立つことが分かりました。暗算でもOK。
数学的帰納法を知っている人はすぐ分かると思います。これ、まさに数学的帰納法の証明の最も肝心な部分なのです。数学的帰納法を説明するのが難しい学校だってありますし、そうでなくても分かりにくいところではあると思います。n=kのときの不等式を仮定してn=k+1のときを証明する。もちろんそれが正しいんですが、授業で難しそうかなと思ったらこの例を出すことにしています。
数学的帰納法の証明は、そうでない証明に比べて「何をやっているのか理解しづらい」と感じることが多いです。もちろん理屈通りなのですが、定理を積極的に成立させる数学の仕組みとでも言うかその辺りがハッキリしないことがあるのです(すみません、うまく表現できない……)。そういうとき今回のような例を見ると「ハハア、なるほど……」となるかも知れません。