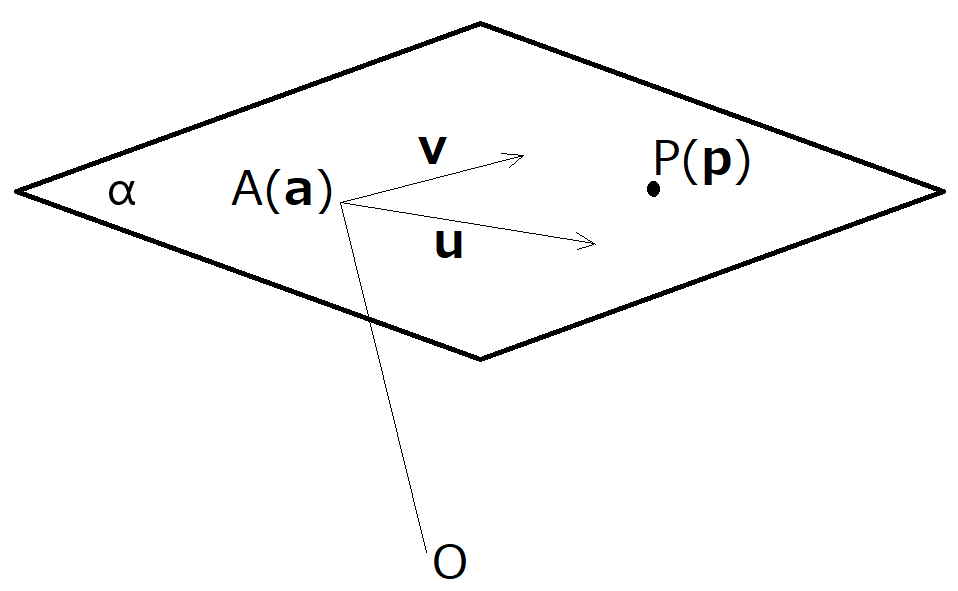
平面の方程式について考えましょう。下の図の平面のベクトル方程式は次のように書けます。Oは位置ベクトルの原点です。
p = a + tu + sv
点Pの位置ベクトルはt,sをうまく決めてやれば右辺のように書ける、ということですね。
x、y、z軸を考えましょう。下は平面y=y1です。
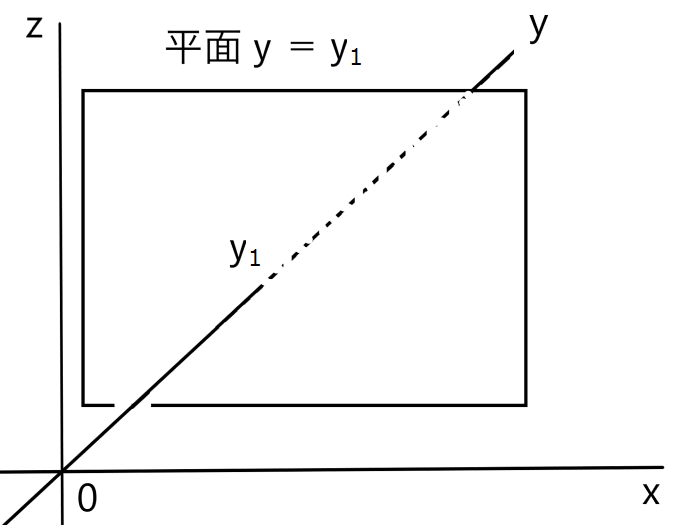
これはzx平面と平行な、点Aを通る平面です。平面αと平面y=y1の交線が下の図のようだったとします。
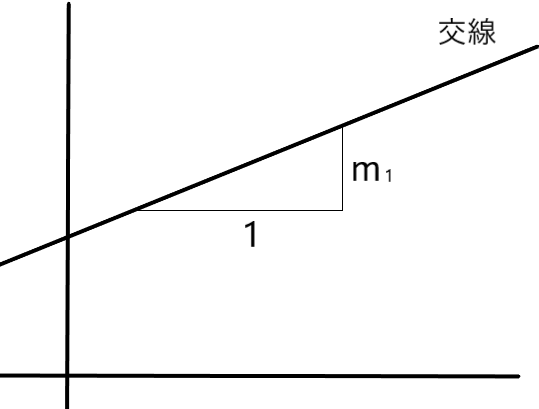
↑ 平面y=y1です
このとき、交線の方向ベクトルはu=(1,0,m1)となります。同様に平面αと平面x=x1との交線の方向ベクトルはv=(0,1,m2)となります。このu、vとa=(x1,y1,z1)を最初の式に代入して少し式変形すると次を得ます。
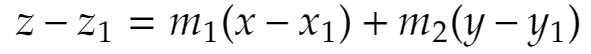
まとめると、これが(x1,y1,z1)を通り、zx平面との交線のzx平面上での傾きがm1、yz平面との交線のyz平面上での傾きがm2である平面の方程式です。
上の式自体はあまり見たことはないかも知れませんが、平面で(x1,y1)を通り、傾きがmである直線は
yーy1=m(xーx1)
なのですから、覚えやすい式ですよね。空間内のこの平面の式は全微分についてまとめようとしているときに出てきました。これについてもちゃんとまとまったら記事を載せます。