今後のこともあるので、ここで合同式についてまとめておきましょう。あの三角形の「合同」ではありません。整数の話です。
ーーーーーーーーーーーーーー
a≡b(mod m)
⇔a,bをmで割った余りが等しい
⇔a-bがmで割り切れる
ーーーーーーーーーーーーーー
が整数a,bが合同であることの定義です。この記号はガウスが導入したそうです。何ということもなさそうな記号ですが、どっこい、これが便利です。要するにそもそも合同の記号がなければ「割った余りが2」というのを式で表現するのが面倒なのですね。それは見通しが悪くなることです。人間が一気に考えられる範囲、深さは以外に狭いものです。記号に言わば「人間が考える代わり」をしてもらうのです。だからプログラムだって「サブルーチン」があるのですね……。話がそれました。
合同式は次の3つの式、同値律を満たします。証明は易しいです。
ーーーーーーーーーーーーーーーーーーーーーー
(1)同一律 a≡b(mod m)
(2)対称律 a≡b(mod m)ならばb≡a(mod m)
(3)推移律 a≡b(mod m), b≡c(mod m)ならばa≡c(mod m)
ーーーーーーーーーーーーーーーーーーーーーー
なお、一般に関係「~」が上の3つの法則を満たすとき、「~」は同値関係である、と言うのでした。例えば「=」は同値関係です。また三角形などの合同「≡」もそうです。大小関係「<」は同値関係ではありません(対称律が成り立たない)。
さて、以下では特に注意の必要がなければ「mod m」は省略してしまいます。合同の定義が分かったら、次は合同式の基本的な性質です。
ーーーーーーーーーーーーーーーーーーーーーー
a≡b,c≡dならば
(1)a+c≡b+d
(2)aーc≡bーd
(3)ac≡bd
ーーーーーーーーーーーーーーーーーーーーーー
証明は簡単です。例えば(1)は
仮定よりa-b=km、c-d=jm(k、jは整数)なので、辺々加えて
a+cーbーd=(k+j)mです。これより言えます。(3)はac-bd=(a-b)c+b(c-d)にa-b=km、c-d=jmを代入すればすぐです。割り算はどうした?と思うかも知れませんが、少しだけ面倒なので後回しです。さて、すると(3)より次がすぐ言えます。

これは大事なことを示しています。例えば
3≡17(mod 7)ですが、このとき
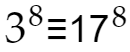
が成立するのです。つまり割り算の余りの計算はどの段階でやっても構わない、と言うことを意味します。
さて、「倍数の判定法」というのがいくつもありますよね。有名なのは「各位の数の和が3の倍数かどうかでもとの数が3の倍数かどうか決まる」とか。つまり258は3の倍数です。それに比べてあまり聞かないのが7の倍数の判定法です。これを考えてみましょう。
以下、mod 7 で考えます。まず1≡1、10≡3。10≡3の両辺に10をかけて100≡30≡2。両辺に10をかけて1000≡20≡-1。両辺に10をかけて10000≡-10≡-3。両辺に10をかけて100000≡-30≡-2。両辺に10をかけt1000000≡-20≡1。以下、繰り返しです。まとめると
1≡1 10≡3 100≡2 1000≡ー1 100000≡ー3 1000000≡ー2
10000≡ー3 100000≡ー2
例えば7812を7で割った余りを考えます。
7812=1000×7+100×8+10×1+2
1000≡-1より1000×7≡(-1)×7≡-7
100≡2より100×8≡2×8≡2
10≡3より10×1≡10≡3
これらと、2≡2を辺々加えると
7812≡7×(-1)+8×2+1×3+2×1 ≡-7+2+3+2=0
よって余りは0です。
ちゃんと書こうと思ってごちゃごちゃしていますが、早い話、各位の数を小さい方から順に1倍、3倍、2倍、ー1倍、ー3倍、ー2倍、1倍、3倍、2倍、……
とかけ算し、結果を加えます。それが7の倍数かどうか調べればよいのです。
高校生のとき参考書に合同式が載っていました。授業では扱っていません。参考書にも7の倍数の判定法だけはあまり書いていません。面倒だから……ということなんですね。