世界中に碁石がいくつあるかは分かりませんが、n個としておきましょう。実は、数学的帰納法を用いて「世の中の碁石n個は全て同色である」……①という事実を証明できるのです。「そんなバカな!?」と思うでしょうが、まあ見てください。数学的帰納法の証明は2段階に分かれるのでした。
-----------
(第1段階)
n=1のとき。碁石は1個なのだから当然同色。よって①は成立します。
(第2段階)
n=kのときに①が成立することを仮定、つまり「k個の碁石は同色である」….…②と仮定します。この仮定の下で、示したいのは「k+1個のときにも同色である」……③ということです。
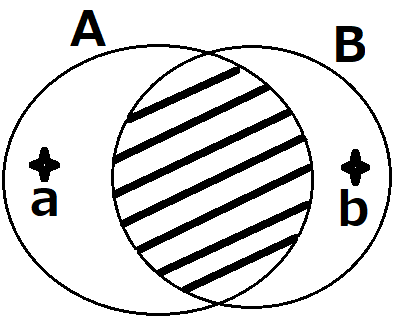
k+1個の碁石の中の2個をa,bとしましょう。aを含んでbを含まないk個のグループAと、bを含んでaを含まないk個のグループBを考えます。Aはk個の碁石のグループなので数学的帰納法の仮定②により同色です。同じ理由でBも同色。図でaは斜線の部分と同色、bも斜線の部分と同色なのだから、結局aもbも同色。これで③を示せました。
-----------
数学的帰納法というのは自然数nについての定理を証明するための強力な方法です。例えば
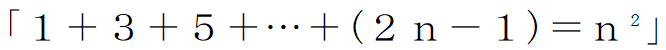
といった定理を証明できるのです。
この話、ぼくは高校生のときに『逆説論理学』(野崎昭弘1980中公新書)で読みました。「面白い話があるもんだなあ~」と思ったことを憶えています。もちろん碁石には黒も白もあるのですから、証明のどこかが間違っているわけです。考えてみましょう!
