ベン図については前の記事があります。4個以上の集合をベン図で表すのは、3個までのときのようにカンではうまくいきません。どうしたらよいのか、その方法をまとめたのでした。
この記事で示したのは「4個以上の集合では、こうすればうまくいく」ということです。見ると分かりますが、最後の集合をクネクネと波打つように描くのです。では、集合が4個以上のとき、集合の境界に円を使うとうまくいかないのでしょうか? うまくいかないのなら、それはなぜでしょうか?
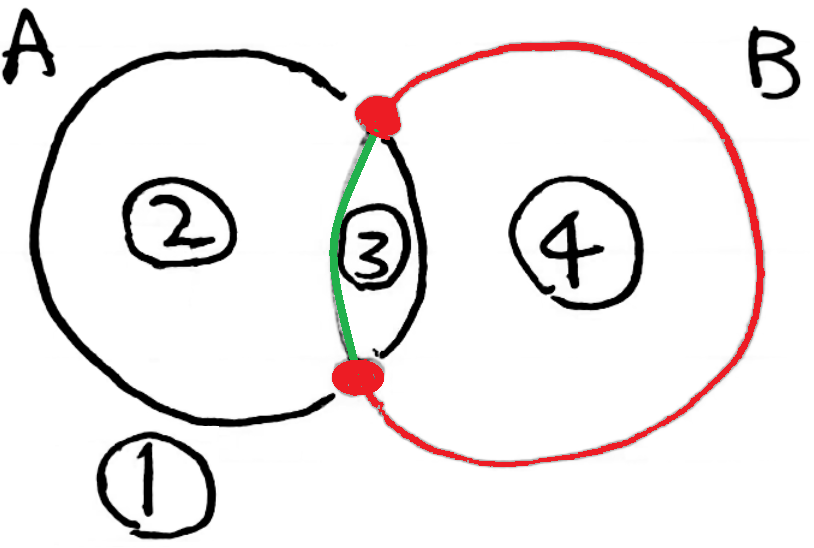
集合がA、Bの2個のとき、上のように平面は①~④の4個の領域に分けられます。集合の境界は円で描いています。ここに第3の集合C(これも境界は円)をつけ加えます。このとき、Cは①~④の4個の領域を全て通らなければなりません。Cの境界は例えば②を2つに分けなければならないからです。そうしないと、②にもCにも属する部分と、②に属するがCには属さない部分ができ上がりません。Cが4個の領域を通るのだから、C(の境界)は上の図の集合Bの境界である緑の線、赤の線を横切らなければならないのです。
さて、今集合A、B、Cがあり、どれも境界は円だとしましょう。平面は8個の領域に分けられています。
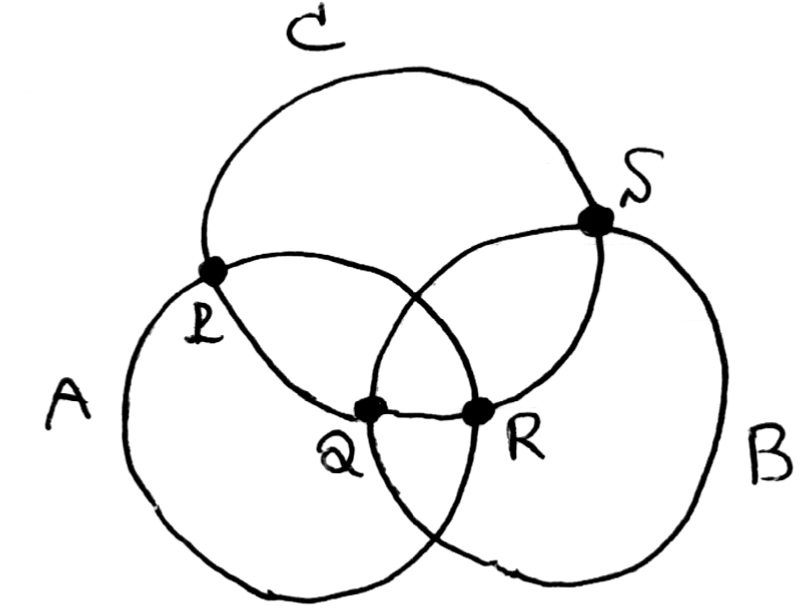
集合Cは境界をP、Q、R、Sの4点で分けられています。弧PQ、弧QR、弧RS、弧SPに分けられるのです。ここに第4の集合Dをつけ加えます。境界は円です。さっきと同じ議論で、Dの境界は4本の弧(PQ、QR、RS、SP)を横切らなければなりません。でもこれは不可能です。円C、円Dは共有点を最大でも2点しか持てないからです。高校2年の教科書の問題です。一応書いておくと……2つの円の交点は方程式を連立して求められます。具体的には、まず2つの円の方程式を辺々引いてx、yの1次方程式を得ます。これは直線の方程式です(2つの円が共有点を持っている場合)。これとどちらかの円の式を連立して、交点が分かるのでした。
以上で分かりました。境界を円で描く場合、集合3個まではうまくいきます。でも4個目はうまく描けません。だから5個目も描けません。