3つの集合A、B、Cのベン図は以下の通りです。こうすれば、例えばAに属するがB、Cに属さない要素も入れる場所はあります。抜けはありません。

では集合4個だったらどうなるのでしょうか。例えば下のようにすると……

A、Dに属すがB、Cに属さない要素が入りません。これではダメです。円でなくてよいので、集合Dのうまい描き方を考えてみましょう。
そのためにまず3個の集合のベン図の、拡張できそうな描き方を見てみます。集合A、Bを描きます。平面は①、②、③、④の4つの領域に分けられます。
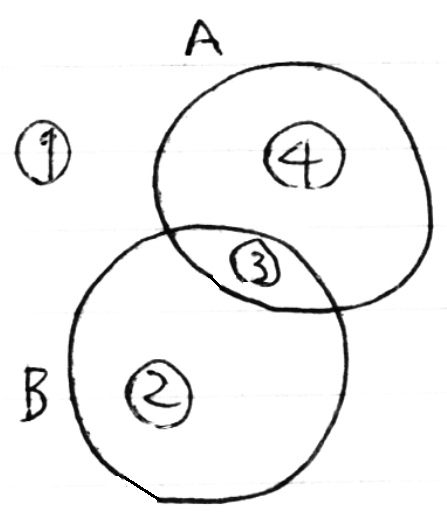
ここに第3の集合Cを描き加えます。下の図では集合Bの境界線を太くしてあります。この境界線に沿って集合Cを描きます。どこからでもよいですが、ここでは矢印の位置からスタートしましょう。太線は集合Aの境界と交わるところが2カ所あります(太線が消えているところ)。この交点によって太線は2つの部分に分けられています。このとき、集合Cの境界線はこの2つの太線を1回ずつ横切るように描けばよいのです。

集合4個のときも同じです。集合A、B、Cを描くと(Cの境界は太線)太線は3つの部分に分けられます。この太線に沿って集合Dの境界を描くのです。矢印のところから始めましょう。3つの太線と1回ずつ交わるようにすれば図のようになります。交点をP、Q、R、Sとしておきました。
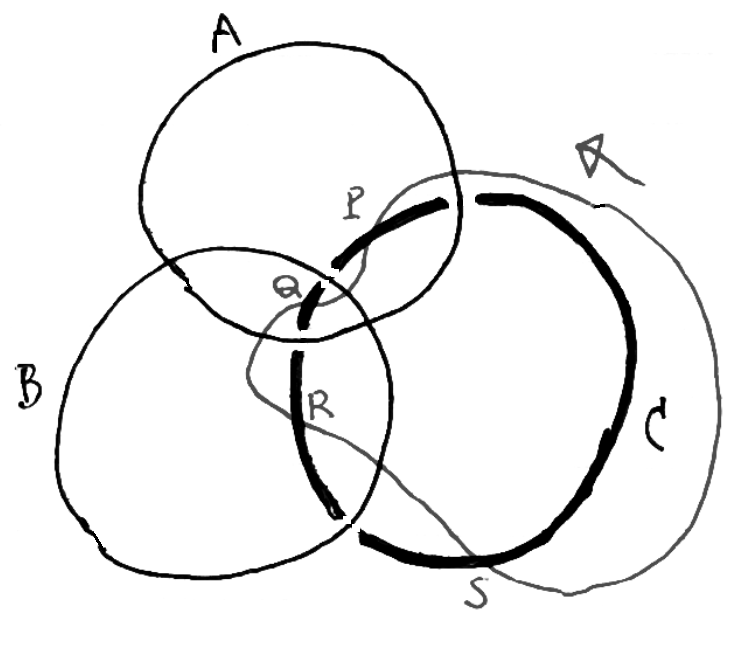
なぜこれでうまくいくのでしょうか。例えば新しい境界がSで交わることによって、
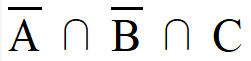
をDに含まれる部分と含まれない部分に分けることができるからです。集合が増えると見づらくなってしまいますが、このやり方なら集合が100個になっても大丈夫です。
念のため、集合の境界は、追加するたびにそこまでにできあがっている領域全てを2つに分けるということに注意しておきましょう。