mが任意の実数値をとって変わるとき、2直線 mxーy=0,x+my-2m-2=0 の交点が描く軌跡を求めます。
1本目はmにかかわらず原点を通ります。2本目は m(y-2)=ーx+2 と変形できるのでmに関わらず(2,2)を通ります。この2本の法線ベクトルはそれぞれ(m,-1),(1,m)ですから内積は0、よって2直線は直交します。円周角が直角であるときは対応する弧は半円になるのでした。つまり、2直線の交点は原点と(2,2)を結ぶ線分を直径とする円を描きます。
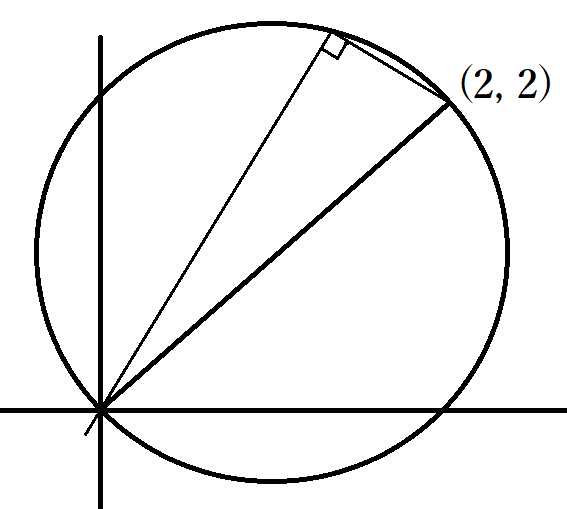
時代もあるのか昔は結構、逆についてうるさく言われたものです。数学で議論するときは、逆がどうなっているのか考えることが大事なケースもたくさんありますから、よいことだったと思います。しかし何だか最近は教科書の書き方も逆については緩くなっている気がします(印象です)。軌跡の問題で「逆に、軌跡上の全ての点は条件を満足する」と書かなくていいのか、気にする生徒も減ったような……。もちろん逆が明らかなケースでは要らないとも言えますが、この問題などは「円周上の点は全て2直線の交点になっている」と言えるのでしょうか? 例えば原点とか、(0,2)あたりは怪しい気がします。
「円周上のどの点も、mをうまく選べば2直線の交点になるか?」、調べましょう。
mを決めれば2直線が決まり、それらはいつも直交しています。だから交点は間違いなく円周上にあります。mをいろいろに変えたときの2本の直線の動きを考えましょう。交点はmの変化に伴い、円周上を動きます。しかし、点(0,2)だけは交点にはなれません。その式の形から、1本目はy軸を表せないし、2本目はx軸と平行な直線を表せないからです。
これで分かりました。軌跡は原点と(2,2)を結ぶ線分を直径の両端とする円から(0,2)を除いた図形です。
そもそも、どうして軌跡の問題で逆について検討する必要があるのでしょうか。条件Cを満たす図形Fを求めるのが軌跡の問題です。軌跡上の点をP(x,y)としたとき、与えられた条件Cからx、yは3x+y=1を満たすことが分かったとすると、軌跡はこの直線(あるいはその一部)だということになります。しかし、ここまでで分かったのは「Pはこの直線上のどこかにある」ということだけです。Pが直線全体に現れる保証はありません。極端な場合には、Cを満たす点は直線上のある1点だけでした、ということだってあり得ます。Cを満たす点は直線の式を満たすけれど、分かったのはただそれだけなのです。だから「軌跡は直線 y=-3x+1 だ!」と主張したければ、逆にこの直線上の点はどれも確かに条件Cを満たしていることを確認しなければならないわけです。
こういうことを細かく考えたがる学生は多分数学が好きなのでしょう。丁寧に相手をしてあげましょう!!