作図の際には定規とコンパスを使う、というルールがあるのでした。ところで定規とコンパス以外の器具を使うとどうなのでしょうか。例えば、トマホークで角を3等分できます。図で太線の部分がトマホークです。
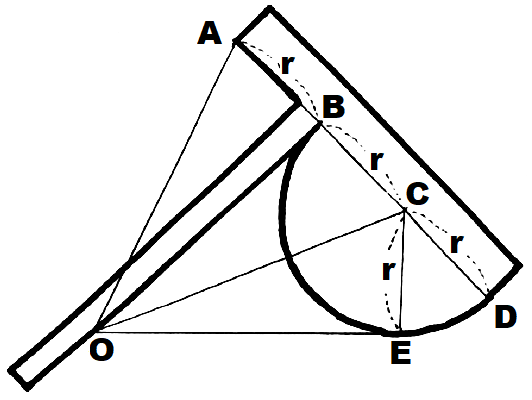
構造から、∠AOEを3等分した角は∠COEとなります(△AOB≡△COB、△BOC≡△EOCより)。つまり、定規とコンパスにこだわらなければ3等分はできるのです。
次に、以降で使う用語を説明しておきましょう。体(たい)とは、四則(和、差、積、商)が定義されている集合です。例えば複素数全体の集合C、実数全体の集合R、有理数全体の集合Qなどがあります。しかし整数全体の集合Zは体ではありません(Z内で割り算が実行できないことがある。4÷3など)。
ある体をもとにして、もっと大きな体を作ることを考えます。Qに例えば√2を添加して(付け加えて)新しい体を作ることができます。Qの要素と√2を自由に足したり引いたり掛けたり割ったりしてできる数たち全体の集合です。この体をQ(√2)で表します。Q(√2)の要素はa+√2b(a,b∈Q)という形で、この形の要素の和、差、積もこの形になります。商も、次のように分母の有理化をすることによりやはりこの形になります。
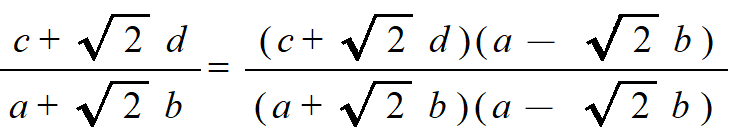
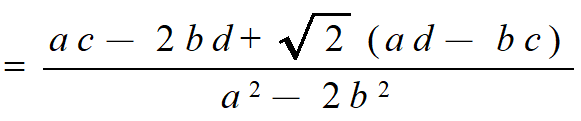
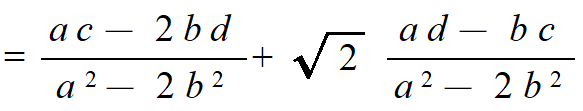
QからQ(√2)を作りました。√2を付け加えて新しい大きな体を作ったので、これを体の拡大と言い、Q(√2)/Q と書きます。また、Q(√2)に√3を添加するとQ(√2,√3)になりますが、このQ(√2,√3)/Q(√2)も体の拡大です。
以降では「解を作図する」という言葉が出てきます。これは「方程式の係数をもとにして、解の長さを持つ線分を作図すること」です。この言葉を用い、いよいよ3等分は不可能であることを証明に切り込みます!
続く!!