A(1,2,3)、B(0,3,2)、C(4,1,2)を通る平面の方程式を求めましょう。最近は高校ではあまり扱わないようですが、ぼくらの頃は授業で出てきました。ここではちょっと変わった……ということもないですが、高校では出てこない求め方を。
求める平面上の点をP(x, y, z)とおきます。このとき、次のベクトル
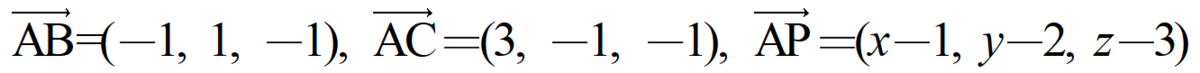
は線形従属ですから、これらを並べた行列の行列式は0です。つまり、

が求める平面の式です。何がいいのかと言うと例えば……まだ計算しなければならない部分はあるにせよ、とにかく一発でその式を表現できる、ということです。行列式を使わない書き方にしたいならこれを展開するだけです。1行目について展開するなら
(x-1)(-1-1)ー(y-2)(1+3)+(z-3)(1-3)=0 ですね。つまり-2(x-1)-4(y-2)-2(z-3)=0……★★です。
外積を使うなら、平面の法線ベクトルは(-1,1,-1)×(3,-1,-1)=(-2,-4,-2)なので、これを法線ベクトルとする、通過点(1,2,3)の平面を求めて★★が得られます。
行列式を用いた★はしばらく使わないでいると忘れがちで、ブログに記録しておきます。特にプログラムのコードなどがそうなのですが、ブログに載せておくと「あれ、どうやって書けばいいんだっけ? 書いたということだけは憶えてるけど」というときに役に立ちます。公開する前提なのでピリッとした緊張感もあり、また、動くことを確認してすぐにブログにあげるので間違いがありません。自分でファイルを1個用意しておき、新しいことをどんどん追加していくのと同じはずなんですが、なかなかそうでもないのですね。例えば、あっちを書き換えて、こっちを書き換えて、とやって少しずつ違ったコードをいくつもセーブしているとどれがまともに動くものか分からなくなったりします。ブログにあげるのはひとつ。2週間経っても「これは間違いなく動く!」と、自分でそれをコピーして使うことができます。
では今回はこの辺で……。
追記 2020.2.4:
もちろん、2次元でも通用する話です。例えば(1,2)、(5,8)を通る直線を求めるとき、直線上の点を (x, y) とすれば
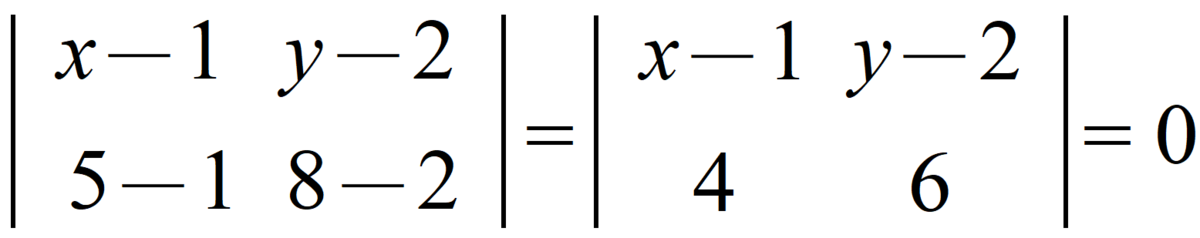
が成立します。これが2点を通る直線の方程式です。