ベクトルの転置(転置行列。ベクトルも行列の一種です)は次のように定義されます。成分は3個にしましたが、何個でも同様です。

さて、今ベクトル a, b, c が次のようであるとしましょう。
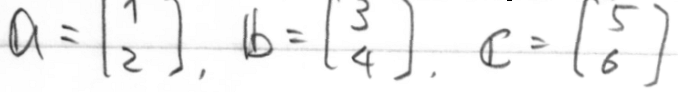
このとき
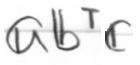
を次の2通りの方法で計算してみましょう。

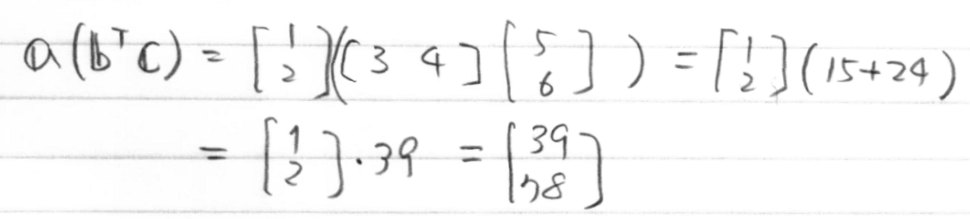
どちらも結果は同じ。しかし、2つ目は? こういう計算をしてよいのでしょうか。kを実数、aをベクトルとして、ka はベクトルの実数倍として定義されていますが、そもそも ak の定義はありません。
そう言えば、工学の本などで、ベクトル a, b(どちらも1行3列) の内積を
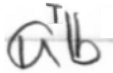
と書いたりするのです。要するに内積を行列の積として計算しています。これ、よいのでしょうか? 「内積はベクトルではない。スカラーなのだ」と強調されることがあります。この計算は行列の積を計算しているのだから結果は行列。(1行2列)×(2行1列)=(1行1列)の行列なんですね。これは「スカラー」ではありません。だから、そういう意味ではやってはいけない計算(行列の積で内積を求める)です。しかし、今まで「スカラー」と思っていたものは実は1行1列の行列なのだ、と考えればよいだけのことですよね。最初の問題も、右から39をかけるのはダメだけれど(39は行列ではないから)、1行1列の行列、[39]だと思えば解決です。つまり
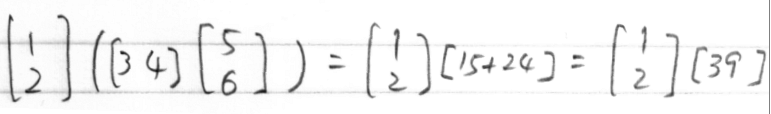
という計算をやっているのだ、と思えばよいのです。行列のかけ算、ABでは、Aの列の数とBの行の数が等しくなければなりません。しかし上の計算ではちゃんと一致しています。(2行1列)×(1行1列)です。こうしたことが分かっているなら、「・39」と書いてしまってもよいかも知れません。何も考えずに計算していてはまずいと思いますが。