平面αを考えます。nはαの単位法線ベクトルです。このとき、rをαに関して対称移動して得られるベクトルr’を求めます。実はこれが四元数につながります。
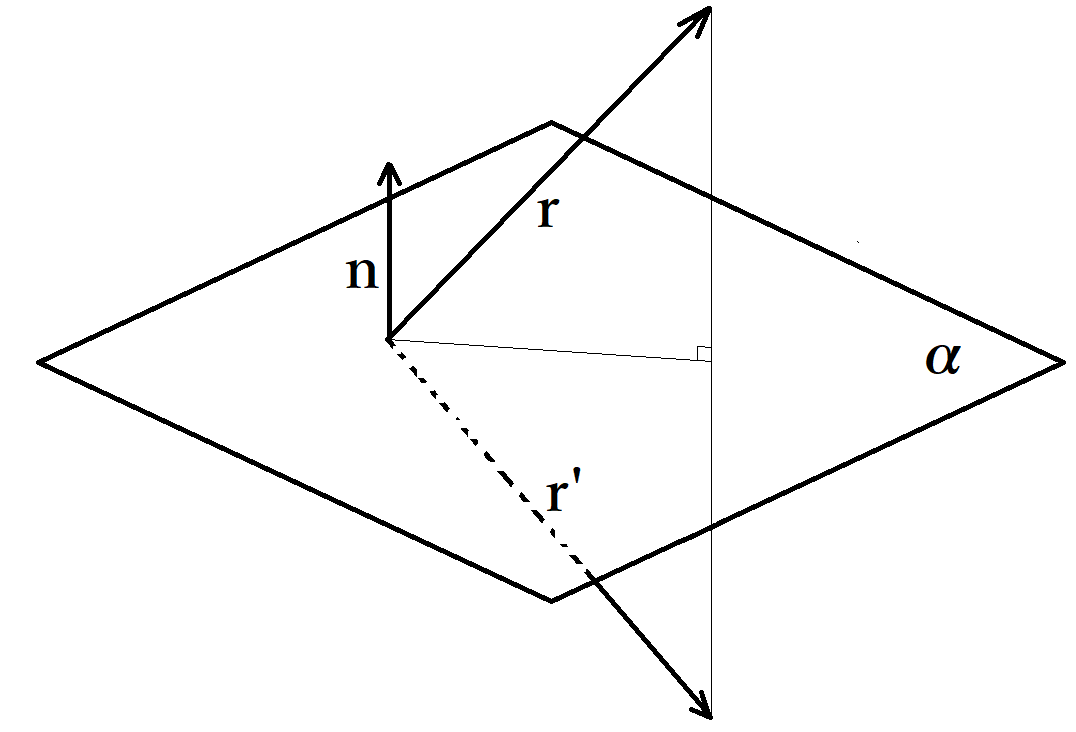
前話題にしたように、rのnへの正射影ベクトルは(n・r)nで得られるのでした。なお「・」は内積を表します。
すると、図からr’=rー2(n・r)nであることが分かるでしょう。
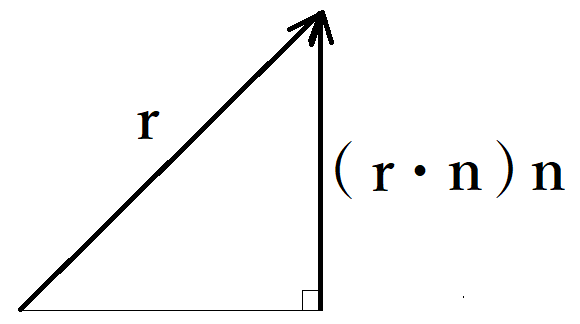
さて、これとは別に、四元数の積を調べておきます。x,yを四元数とします。

前回書いた
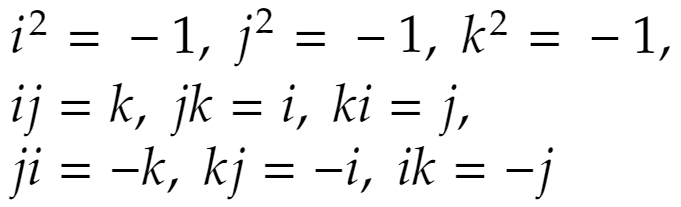
を使いながら、四元数の積xyを計算してみます。なお、四元数は積については交換法則が不成立となります。それを除けば複素数と同様に計算できます。実際に計算してみると

が得られます。これを見やすく、次のように書き直します。
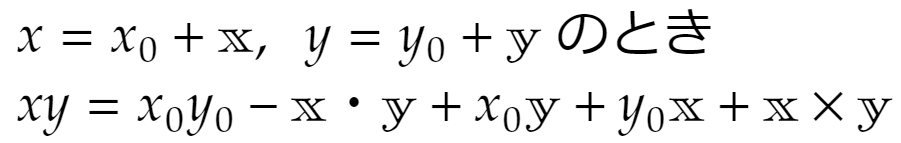
なお×は外積です。ここではベクトルに2重線を使ってみましたがずっと上で使っている太字のベクトルと思って下さい……。
次に四元数N、Rを N=0+n、R=0+rとします。このn、rは記事の前半で話題にしたものです。このとき上の積の式から
NR=-n・r+n×r
NRN=(-n・r+n×r)(0+n)
=-(n×r)・nー(n・r)n+(n×r)×n
ここで (n×r)×n=0 、また (n×r)×n=rー(n・r)n なので、結局
NRN=rー2(n・r)n=r’ であることが分かります。
なお (n×r)×n=rー(n・r)n は外積、内積について成立する公式です。ベクトル解析のテキストなどに載っています。
まとめておきましょう。
nを法線ベクトルに持つ平面に関してrを対称移動するとr’に移るとする。
四元数N、Rを N=0+n、R=0+r とするとき
r’ =NRN(=rー2(n・r)n)である。
次回、これを用いて空間内の回転を四元数で表してみます。