マクローリン展開というのがあります。高校生の頃、
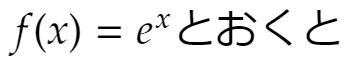
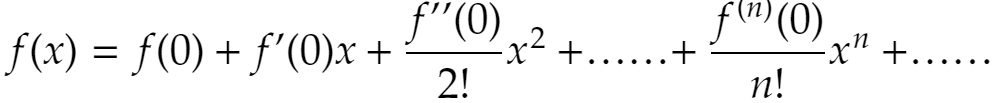
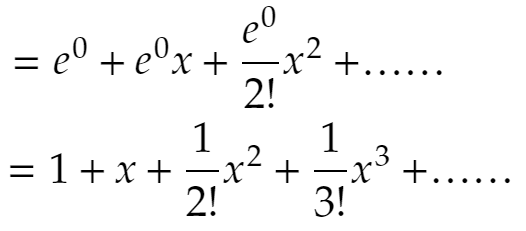
というのを見て衝撃を受けました。関数によっては(というか、大抵は)値を求めるのは難しい。指数関数も三角関数もそうです。しかし、マクローリン展開を使えば(関数電卓ではない、普通の)電卓で計算できる。これは凄い、と思ったのです。雑な証明でよければ、指数関数を係数が不明のxのべき級数で表しておいてこれを繰り返し微分することでマクローリン展開はすぐ得られます。無限項の和を微分してよいのか(項別微分してよいのか)など、厳密なことは高校生の頃は知りませんし(そういうことを気にしなければいけない、という発想自体がない)、そうすると展開式を導くことは楽なのです。高校でも元気な(?)先生が理系の生徒に授業で説明することは珍しくないでしょう。「数学って凄い!」と宣伝するのによいテーマなのかも知れません。
大学に入り、最初に微積をたたき込まれるわけですが、そこですぐにテイラー展開、マクローリン展開が出てきます。そのとき「本当にこんな展開をしてよいのか」厳密に考えなければいけないのだ、と反省を迫られます。そこでまた「おお、なるほど! 今までは雑に考えていた!!」と、これも衝撃でした。
ちゃんと議論するなら……
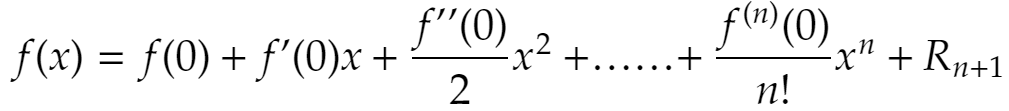
をマクローリンの定理と言います。最後の項は剰余項と言い、xの整式とは限りません(大抵違う)。これがn→∞のときに0に収束すれば先のマクローリン展開が可能、ということになるのでした。剰余項は実は次のように表せます。
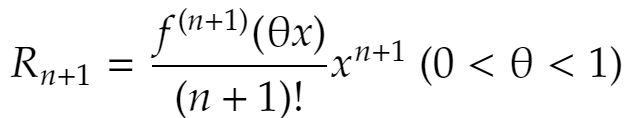
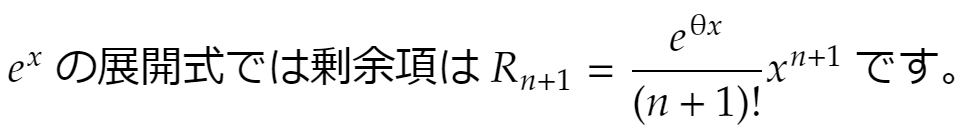
これが0に収束することを示しましょう。そのため、まず次の事実を証明しておきます。
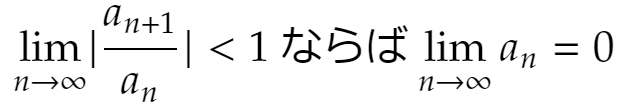
(証明)
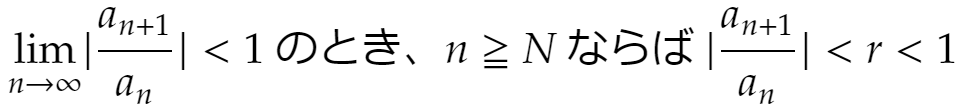
となるNが存在するはずです。これより
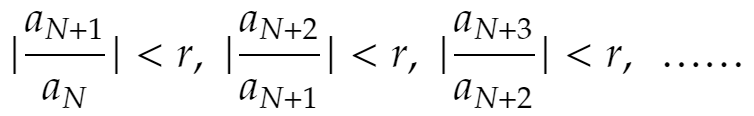
が成立。よって
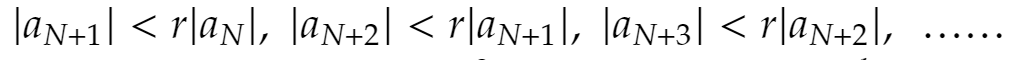
これより
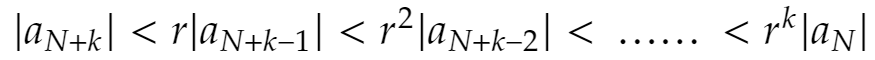
よって
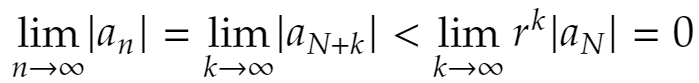
(証明終わり)
剰余項の式から
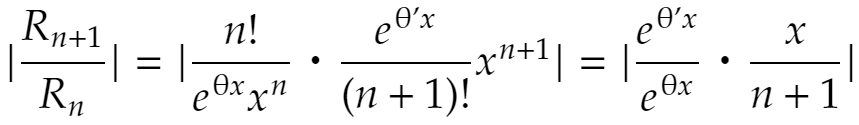
よって

なので、先の定理より
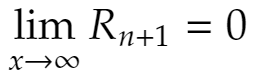
が成立します。
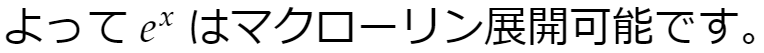
なお、nが変わると剰余項のθも変わることに注意しましょう(証明ではθ、θ’としている)。また、nが変わっても0<θ<1であることは変わりません。これにも気をつけてください。
さあ、これで堂々とマクローリン展開できるようになりました!! 高校で話すときには「実は本当にこういうことをしていいのか、それは大学で習います」とつけ加えてもよいでしょう。夢のある話ですから、取り上げるのはよいことだと思います。