自然対数の底を e とすると、前回のマクローリン展開によれば

なのでした。xはどんな値でも収束です。x=1とおいてみると

です。これは実は無理数です。証明しましょう。この証明は何回か紹介している数学ワンポイント双書の『テイラー展開』(渡部隆一1977共立出版)によります。分かりやすく、多分名著と言ってよいのではないでしょうか。
さて、
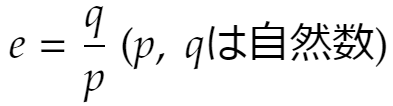
であるとしましょう。あとで必要になりますが、q>1であることはいいでしょう(q=1だと q/p = e にならない)。等式
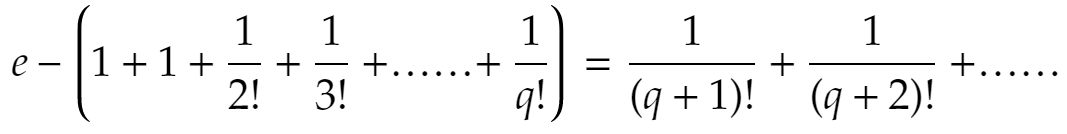
の左辺をA、右辺をBとおくと、q!A は自然数です。一方、
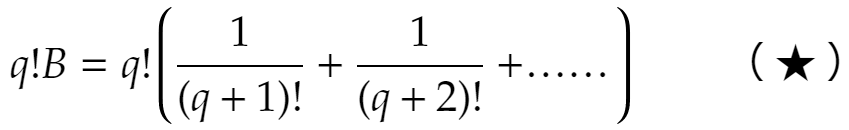
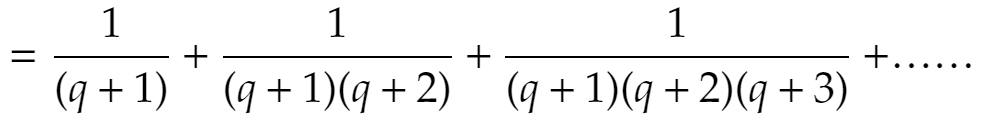
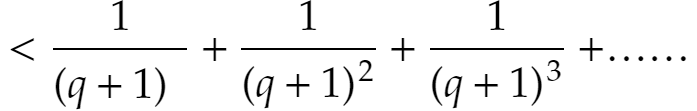
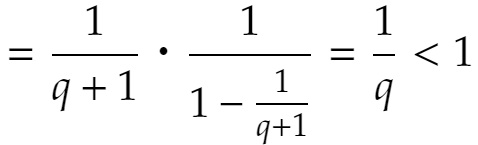
ですから q!B は自然数ではありません。これはA=Bに反します。よってeは有理数ではありません。すなわち無理数です。
なお、★のところでq! をかけています。収束する級数に定数をかけるときにはその定数を分配できるのでした。
うーん、面白い。こういうのを見るとやはり数学は面白いと思ってしまいます。
