方べきの定理というのは、いくつかありますが例えば下の図で PA・PB=PC・PD ……★が成立する、というものでした。もちろんこれで正しいですし、難しい問題の中でも多分無事に使えると思います。
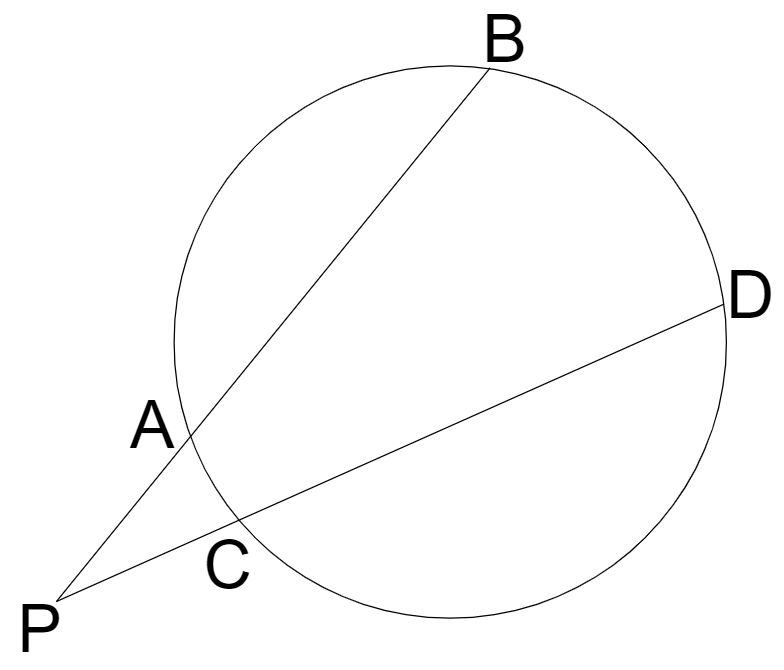
そうなのですが、ときとしてこういう見方も必要です。
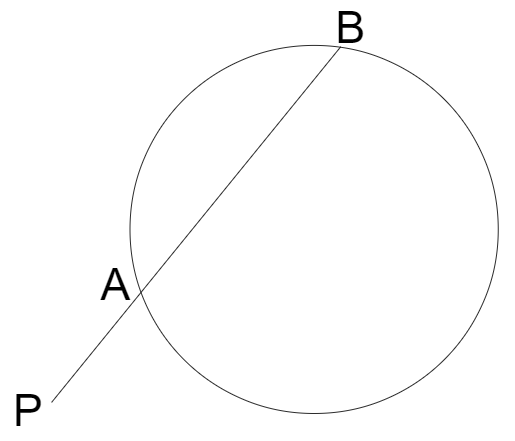
線分が円を横切っているとき、線分がどこにあろうがPA・PBは一定です。★はこういうことを主張しています。当たり前のことですよね。でもあまりこういう表現は見かけません。証明するときは★の形の方がしやすいでしょうから定理としてはこれで載っているのかも知れませんが、「PA・PBは一定」という見方だって大切だと思います。
同じことは正弦定理でも。図で
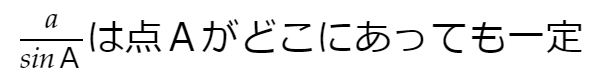
というのが正弦定理です(そしてその「一定」である値は外接円の直径なのでした)。
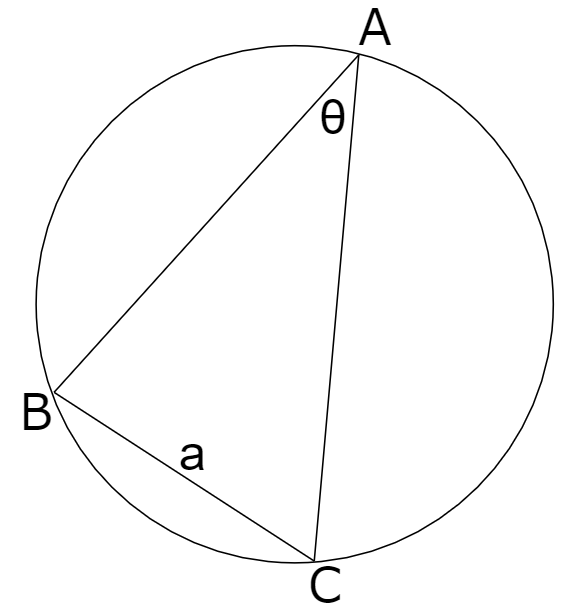
同じと言えば同じ。それはそうですが、聞く人によっては「ああ、そういう意味の定理なんだ」と思うことがあるかも知れません。ちなみにぼくは方べきの定理については「おお、そういうことなんだ」と一瞬、感心しました……。