Bachet(バシェ)の定理について書きます。高校ではここまで扱うことは少ないでしょう。後でこれを使って合同式の簡約公式などを示します。なお (x, y) で x, y の最大公約数を表すことにします。
ーーーーーーーーーーーーーーーーーー
Bachetの定理
文字を全て整数とします。このとき、
ax + by = 1が整数解を持つ ⇔ (a,b)=1
ーーーーーーーーーーーーーーーーーー
証明:
(右向き) (a, b) =d(≠1) とすると、方程式の左辺はdで割り切れ、右辺は割り切れない。よって(a, b) =1 でなければならない。
(左向き)
ユークリッドの互除法でa,bの最大公約数を求める手続きを実行します。
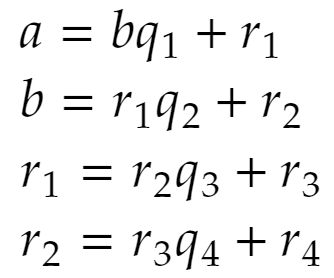
このとき、
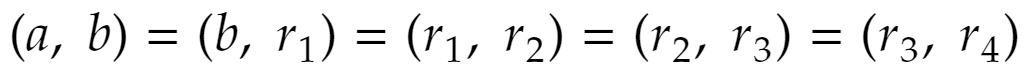
で、もともとa,bは最大公約数が1なのですから、
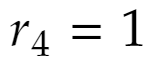
でなければなりません(……★ ここまで徹底的に互除法を実行)。ここで

a×○+b×□=1 という式が得られます。これでx=○、y=□という整数解があることが分かりました。
なお、真面目に代入して式変形、と繰り返さなくても、
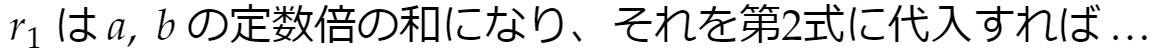
という感じに考えればすぐ分かります。それと、互除法の式はもちろんもっと増えたりするかも知れませんが、やることは同じです。理屈が分かればよしとしましょう。愛読書、『親切な代数学演習―整数・群・環・体』(加藤明史2002現代数学社)では右向きの証明を数学的帰納法でやっています。証明の仕方はいろいろのようです。
高校のとき、2x+3y=1 のような不定方程式の解き方を勉強して大変新鮮に感じました。勉強し始めの頃って、よいものですよね。ワクワクというか、「おー、これは凄い!」とか。いつもこういう気持ちで取り組みたいものです……。
追記:
★のところ、疑問に思った人がいるかも知れません。説明しておきます。