調整中!
これでは証明になっていない……。なんとかします。
収束する、正項である数列の和を考えます。この数列を下の表のように並べ替えます。並べ方は問いません。
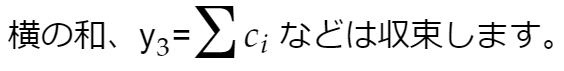
収束する正項級数から取り出したわけで、上に有界、単調増加だからです。
さて、皆さん「明らか」と思っているからなのか、タイトルの「正項級数はどこからどう加えても和は一致するか」については見かけません。もう少し具体的には、「正項級数は、どう並べ替えても、その上でどこにどう括弧をつけても(括弧は有限個でも無限個でもよく、カッコ内の項数は有限個でも無限個でもよい)和は変わらない」ということについての議論をあまり見たことがありません。ずっと気になっていたので、ここでハッキリさせておきます。単に並べ替えた数列に関しては和は一致することは様々なテキストで証明されています。微積分の本に載っています。この事実を使います。
さて、問題の正項からなる数列から項を自由に選んで和をつくり、括弧をつけて
(…………)+(…………)+(…………)+……………… (★)
という和を考えてみます。もちろん1回選んだ項はもう選べませんし、選ばない項があってはなりません。こうしたとき、この和はもとの和と一致するのでしょうか。
最初の括弧の内容を表の1段目、次の括弧を2段目、……と数列を配置します。有限項しか入っていない括弧があれば0を補います。★の和を計算することは、下の表で
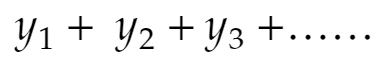
を求めることです。各項が収束することは最初に確認しました。

青字に注目してください。ジクザグに加えた和を
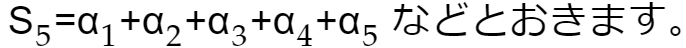

なおこのSはもとの級数の和のSです。ジグザグの和は、もとの級数の並べ替えの和だからです。
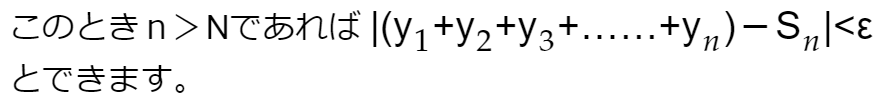

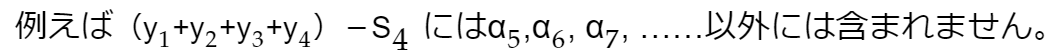
具体的に式を書いてみればすぐ分かります。
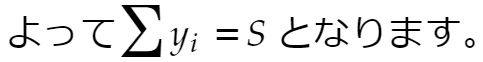
もともと
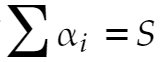
だったのですから、これは★の数列の総和がSであることを意味しています。
雰囲気だけを書くと……もとの正数からなる数列を勝手に並べ替え、括弧も好きなようにつけます。括弧ごとに和を計算し、それらを総和することはジグザグに和を計算することと同じです。もともと、正項級数は順番を変えても和は変わらないという性質がありましたから、ジグザグの計算は順番を変える前の数列の和と一緒です。
……と、こうなります。以下の本の2重級数についての定理の証明が参考になりました。
追記:
アップ後にあちこちにミスが見つかり、直すのが大変でした……。何かまだお気づきでしたらお教えください。
