こんなのをあみだくじと言いました。
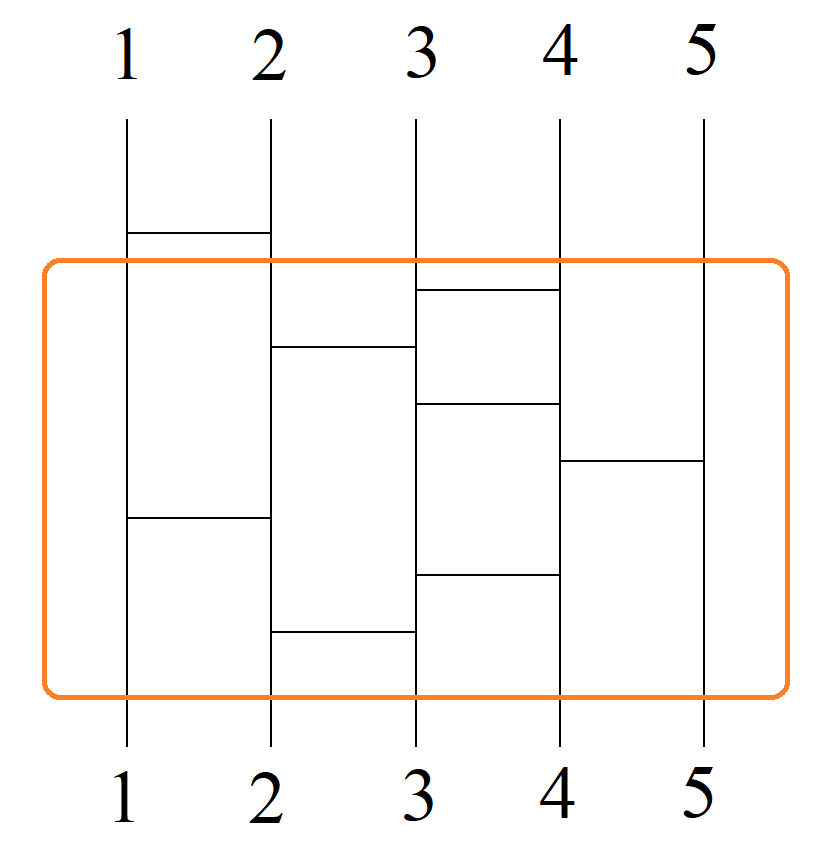
この例では、例えば上の1を選ぶと下の5が当たります。このあみだくじ、縦線が何本でも横線が何本でも、必ず異なる番号は異なるゴールに対応します。例えば 1→5、2→5 などと対応してしまうことはありません。なぜでしょうか。
厳密には例えば横線の本数に関する数学的帰納法で証明することになります。以下の通りです。
まず、横線は高さをみな違えておくことが可能です。上下に多少ずらしてもくじの機能に変わりはないからです。
(第1段階)横線の本数が1本のとき、2カ所が入れ替わるだけですから明らかでしょう。
(第2段階)横線の本数がk本のとき、定理の成立を仮定します。つまり「横線の本数がk本のときは同じ場所にたどり着くことはない」と仮定します。図のオレンジ色の線で囲まれた部分を横線の本数をk本だとしましょう。この囲いの部分については同じゴールにはたどり着かない、というのが仮定です。k+1本目がオレンジの囲いの上にありますから、上の図で言うと縦線の1本目と2本目が入れ替えるだけですから、結局違うスタートから同じゴールにはたどり着きません。
数学的帰納法は、自然数に関する定理の強力な証明法です。高校では2年生くらいで出てきます。初めて授業するときは「n=kのとき正しいことを仮定するけれど、そんなことしていいの?」という質問がたいてい出ます。説明の仕方はいろいろでしょうが、ぼくは「n=kのときは正しい、と言っているわけではありません。正しいと仮定すると、と言っているだけです」と話し、「第2段階は
『n=1で成立ならn=2で成立』……①
『n=2で成立ならn=3で成立』……②
『n=3で成立ならn=4で成立』……③
………………
という無数の定理を一気に証明していることになります。第1段階でn=1のときには正しいことが分かっていますから、これと①を組み合わせてn=2で成立することが分かります。これと②を組み合わせてn=3で成立することが分かります。……と繰り返せます」
と続けます。
数学的帰納法についてはこんな記事も書きました。
生徒にはよく紹介します。面白い話です。