次の問題を考えましょう。
--------------
ダムに取り付けてある1辺の長さa(cm)の正方形の窓(穴)から毎秒流れ出る水の量はいくらか。ただし、正方形の水面に近い1辺は水面下b(cm)のところにある。また、深さx(cm)の小孔から流出する水の速度は
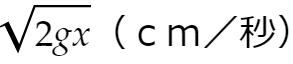
(ただしgは重力加速度)である。
--------------
後半の「√2gx」というやつは物理の知識です。これは認めておきましょう。図を見ながら考えてください。
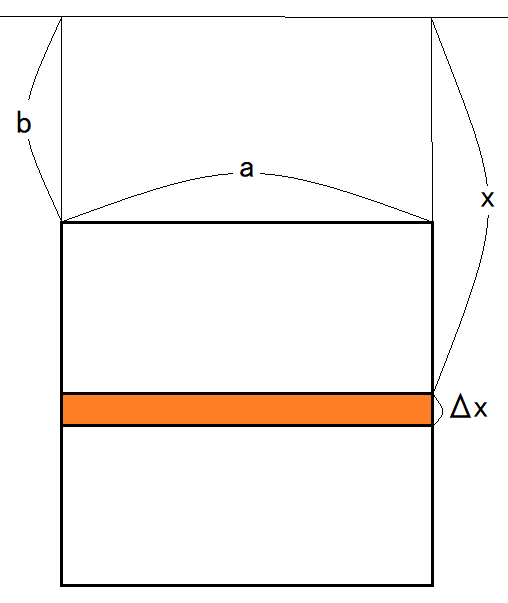
オレンジ色の部分から1秒間に出る水をΔV㎤ とします。Δxが小さければ
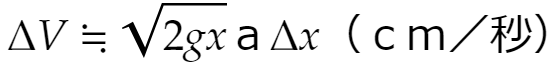
が成立します。窓の面積はaΔxだからです。従って、1秒間に窓全体から出る水の量Vは(窓の高さはx=bからx=a+bまでなので)
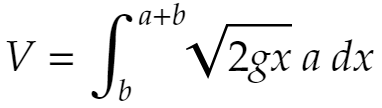
となります。「量の求め方の原理」ですね。この先の計算の過程はまあいいでしょう。当時高校生だったぼくは、こうして世の中のいろいろな現象を数学を使って調べることができるということを知って驚いたものです。近似的に×××が成立するから積分して……というあたりが特に印象的で、もう物理などやっているといくらでも出てきます。『ガリレオ』に出てくる湯川学先生も毎日こういう計算をやっているんだろうなあ、とかときどき考えています。隣の席の友だちがΣを∫に変える部分(横長の長方形で水の量を求め、それを上から下まで加える。これを、幅を小さくして積分で実行)のことを「あんなこと、やっていいの?」と言っていたのを憶えています。その通りですよね。突っ込まれると困るけれど、とりあえずいいでしょう。あんまり神経質になると疲れます! 端的に言うと、小さな変化については単純な比例式が成立する、とでもなると思います。Δxが十分小さくなければあんな近似式は不成立です。小さいから単純にΔxをかけて計算できるわけです。これによって数学や物理の世界が広がりました。
この問題は『演習 微積分(Ⅱ)』(春日正文1979科学振興社モノグラフ新書)に載っています。高校時代、これで微積分の勉強をしていました。
一応計算結果を書いておくと
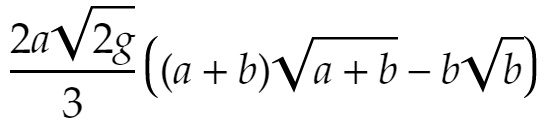
です。
物理の問題で微分方程式を立てるときなどにもΔxはたくさん出てきます。解くのは大変なのが多いですが立てるのは面白い! こんな話もまたいずれ。