この前、スーパームーンが話題になりました。これから書くのは数年前のスーパームーンの話です。平成28年11月14日の夜は月が地球に最接近しました。月は地球の周りを楕円軌道を描いて回っており、離れたり近づいたりするのです。一番離れているときには40.7万km(=Rとおく)、スーパームーンのときは356511km(=rとおく。今回の値)だそうです。一番離れているときの14%増しの直径、面積は30%増しになるとか。「ホントか?」と思って計算しました。月の直径をL=3474km(ネットで調べた)としましょう。
ニュースで言う「直径」というのは、「地球から月を見たとき、月の端から端までの角度」の意味でしょう。つまり図のα、βです。α、βはラジアンで測ります。
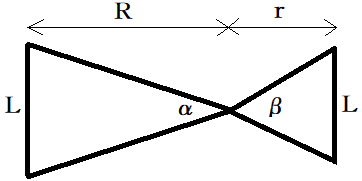
このときL≒Rβ、L≒rαと考えていいでしょう(Rβは、厳密には半径R、中心角βの弧の長さ。半径と中心角から弧の長さ求める公式です。Lと弧の長さは近いでしょう)。すると
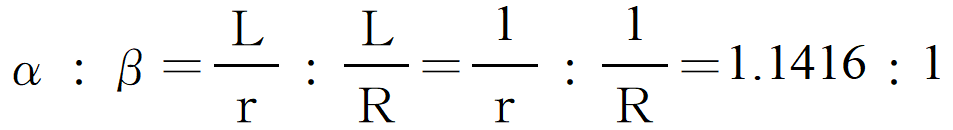
つまりα≒1.14β、よって「直径」は一番小さいときの14%増しに見えるわけです。直径が14%増しなのだから面積は
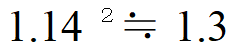
つまり30%増しになるのです。もう少しちゃんと計算したい人は次を。
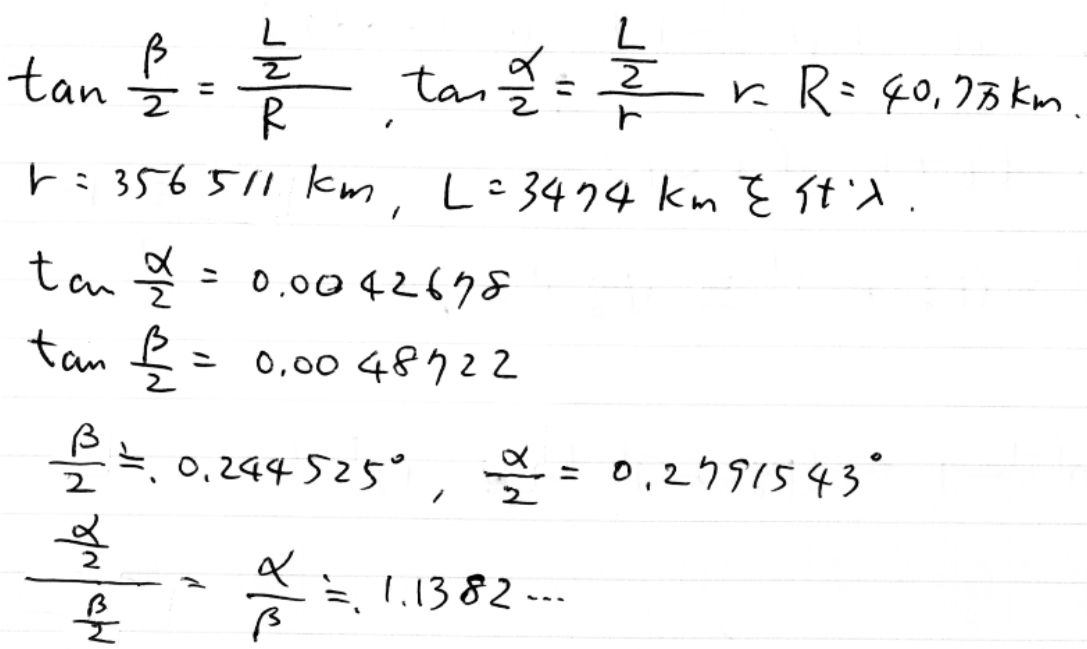
こちらの計算でも角はおよそ14%増し。簡単な計算です。でも自分でやってみることが大事です。ニュースを鵜呑みにして「14%」と思い込むのとは雲泥の差、こうして手に入れた知識こそが本物です。