図のAからBまで光が進みます。x軸より上の部分は屈折率がn、下の部分はmだとしましょう。Aから出た光がPで屈折してBに届きます。このとき光の通るルートを求めてみます。これに関してはスネルの法則というのがあり、これを使えばすぐです。でもそうではない、ちょっと面白い考え方で角α、角βの関係を調べます。場合によってはこちらの方が自然界の本質を突いているのかも知れません。
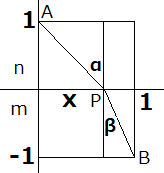
真空中での光速をcで表します。このとき物理学の教えるところによるとそれぞれの媒質中での光速はx軸の上側ではc/n、下側ではc/mになります。するとPを経由してBにたどり着いたときの所要時間は
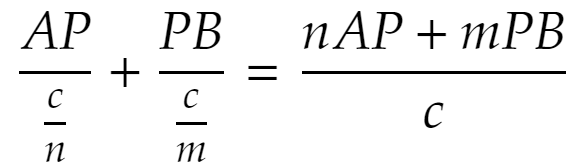
です。ここで分子を
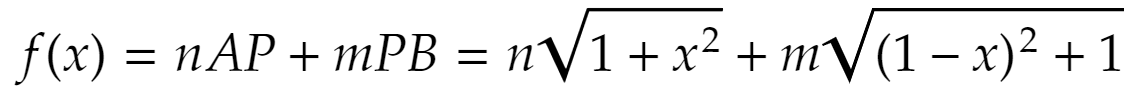
とおくと、導関数を調べて
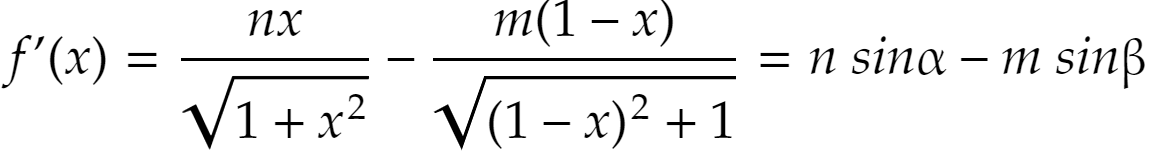
が分かります。仮に「光は所要時間が最短になるルートをとる」が成立するとしましょう。この問題の場合、導関数の値が0になるのは所要時間が最小になるときだと考えられますから、結局
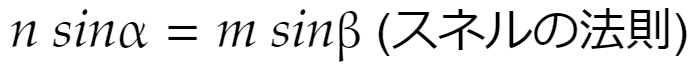
のときに所要時間が最小、と分かります。
出てくる結果はスネルの法則で、そもそもスネルの法則自体は「光は所要時間が最短になるルートをとる」を仮定しないで出てくるのですから、多分この仮定は正しいのでしょう。不思議な事実と言えます。「どうしてそんな仮定をしていいの?」と聞かれると困りますが、こんな単純な事実を仮定しただけでよい結果が出るのです。物理学的にきっと大事な意味があるのだと思います。
自然界がうまくできているのか、物理が凄いのか。何にしても、ぼくが「物理って面白い」と感じるのはこんなときです。……しかし、この仮定を置くと一気によい結果が出るというのは、この仮定が物理現象にきつい制限を加えていることをも意味します。光の立場としては「そんなメチャクチャなこと言われたら結果はこうなるに決まってるでしょ」とでも言いたい場面なのかも知れません。……なんて考えるのも面白いものです。