正の有理数全体の集合をQ+としましょう。Q+は可算集合です。つまり、正の分数全体に1番、2番、3番、……と番号をつけることができます。まずこれを示しましょう。前の話に従うと「NとQ+は同じ濃度である」ということです。 平たく言うと、正の分数は自然数と同程度の数しかない、ということです。
こんな表を作ります。この表には正の分数(正の有理数)が全て、どこかに現れています。
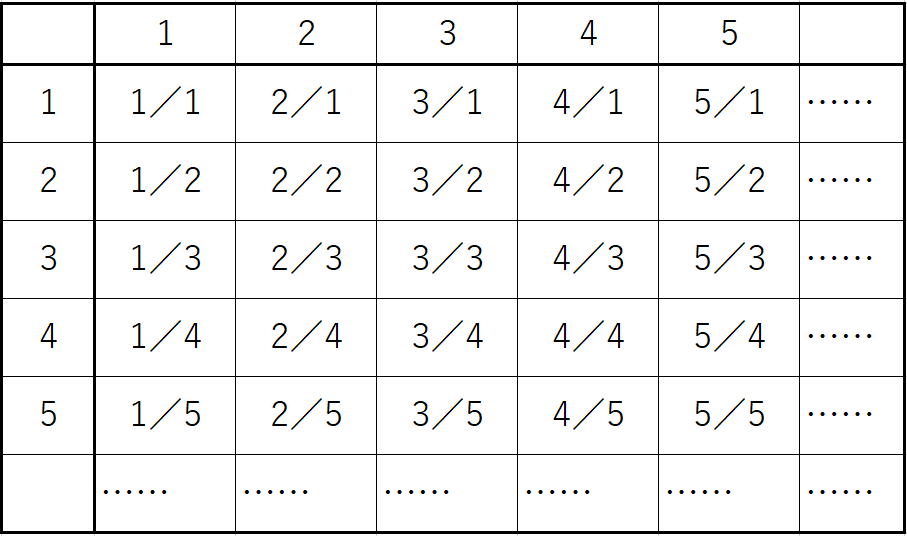
これら正の有理数たちに番号を振ります。
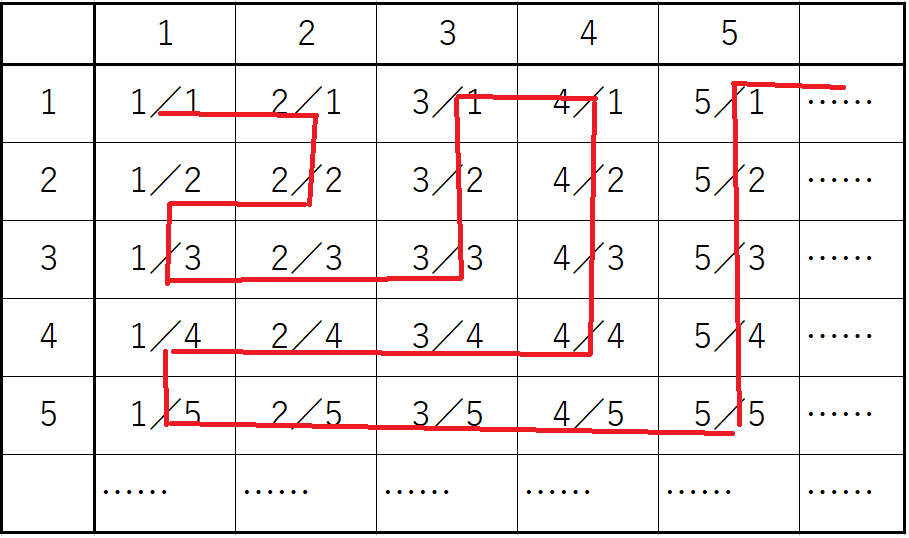
赤い線の順に、有理数に1番、2番、……と番号を振ってゆくのです。途中、1/1と2/2や1/2と3/6のように同じ分数が現れますが、同じものが出てきたら番号はつけずに飛ばすことにします。これでQ+はNと1対1に対応がつき、濃度が同じだと分かりました。
続きです。可算集合Aに有限個の要素を追加してもやはり可算です。実際、

に例えば3個の要素b,c,dをつけ加えると
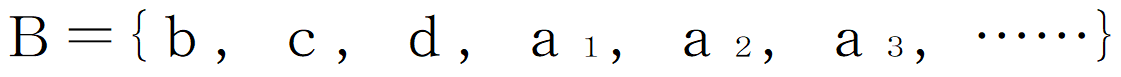
になり、Bの要素に改めて先頭から1,2,3,……と番号がつきますから分かります。さらに可算集合Cを用意します。
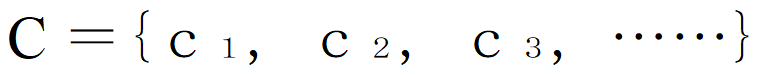
このときA∪Cも可算集合です。
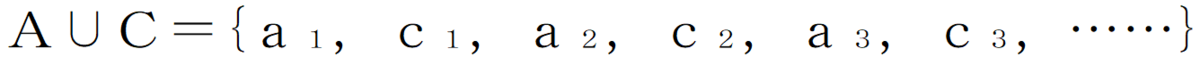
なので、改めて先頭から順に1番、2番、……と番号をつけられるからです。
負の有理数全体の集合Q-はQ+と同様、可算集合ですから、上に書いたことより(Q+)∪(Q-)は可算集合です。すると再び上に書いたことよりQ=(Q+)∪(Q-)∪{0}は可算集合です。
実数全体の集合Rは実は可算集合ではありません。可算集合より言わば「要素がたくさん入っている」集合なのです。不思議な話です……。