高校では真数(log x の x の部分)は正、ということになっています。
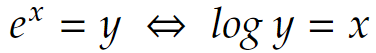
で log を定義しており、xにどんな実数を入れてもy>0であって、だから真数>0なのでした。
大学へ行くと次のオイラーの公式を習います。
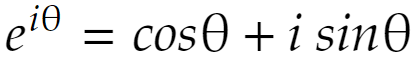
i は虚数単位です。θ=π+2nπ(nは整数)を代入すると、
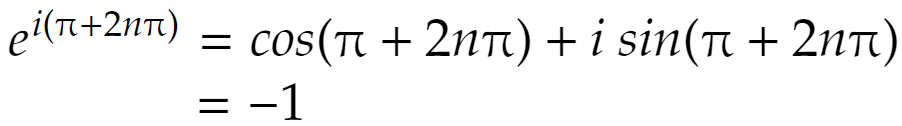
なので(そして log の定義は高校の時と同じなので)、
log(-1) = (π+2nπ) i
となるのです。
理系だとオイラーの公式くらいは知っている生徒もいます。理屈は別として、啓蒙書なんかに「こういうキレイな定理があります」みたいな説明があって、読んでいたりするのです。高校生は「真数は正!!!」とたたき込まれていますから、「大学に行くと真数が負になることもあるんだよ」と話すと「えー!?」とビックリします。驚かせた上で「オイラーの定理って知ってる人もいるでしょ? …………」と説明します。
ぼくは授業で結構、いわゆる「雑談」をするのですが、1日に2つくらいは何か、この手の話を入れることにしています。ブログに書くような話です。実際のところ、そうしてもしなくても変わりはないのかも知れません。しかし自分が高校生だったらいろいろ話してくれる先生に教わりたいと思うので、ぼくはタイミングを見てやっています。
何回か書いていることですが、丁寧に「教え方」を教える大学があるみたいです。実習生を持つと感じます。模擬授業もやるそうです。でも、「どうして数学を勉強するのか」とか、「どのように数学が使われているのか」とか、「今、勉強していることが大学でやる内容にどうつながるのか」とか、そんなことは放っておいて、「どう教えれば分かりやすいか」、「生徒同士の対話が大事」しか考えていないように思います。アンケートをとって確認したわけではありませんが。
実習生を持つときは、必ず「数学通信」を書かせます。面白そうなテーマを選んで生徒に向けてB4版くらい、週に1枚。でも実習生はなかなかいいものは書けません。「分かりやすい授業」しか考えてこなかったならそうなるでしょう。何を書いたらいいのか、分からないみたいです。テーマなんか、いくらでもあるのにね……。
せっかく授業をするのだから、(分かりやすいというのは大事だけれど)何かいい話をしてあげればいいのに……と思います。
そう言えば……ぼくたちは高校の頃、「真数>0」を「真数条件」と習いました。今はこの用語、教科書に載っていません。なくなったんでしょうか?