
nは自然数です。オイラーは上の形の数は必ず素数になると信じていたとか。しかし後に

が示されてしまい、予想は成立しませんでした。これに関しては、次が成立します。
ーーーーーーーーーーーーーーーーー

の形の数(mは自然数)は、もしも素数であるとするとmは2の累乗である。
ーーーーーーーーーーーーーーーーー
しかし、逆にmが2の累乗だからと言って、必ず素数になるというわけではないのです。実際、先に示したような素数にならない例があります。では定理を証明してみましょう。
対偶を示します。つまり、「mが2の累乗でなければ★は素数でない」を示します。mが素因数2以外を含むとしましょう。証明は同じようなものですから、m=10であるとしてみます。このとき

A+1≠1ですから、上の式が素数であるならば次の式が順に成立しなければなりません。

これはありえませんから、結局
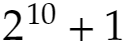
は素数ではありません。以上です。もっとよい示し方があるでしょう。思いつきでやっています。
梅雨に入ってしまいましたが、コロナはどうにか収まって(まだまだ危なそうですが……)学校も一応スタート。若い人たちと話をするのはやはりよいものです。元気が出ます。