前回、中心力の仮定とケプラーの第1法則(惑星は楕円軌道を描く)から万有引力が距離の2乗に反比例することを示しました。
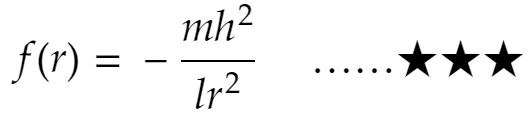
rは焦点からの距離、mは惑星の質量、hは面積速度の2倍(面積速度はh/2でした)、l(小文字のエル)は軌道の半直弦の長さです。
今回はここへさらにケプラーの第3法則を用い、万有引力の式をもっときちんとした形で求めます。まず楕円について復習です。
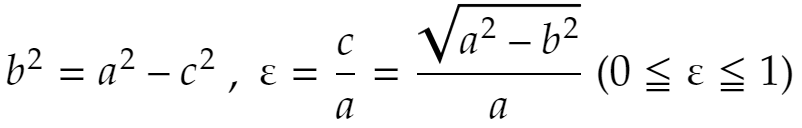
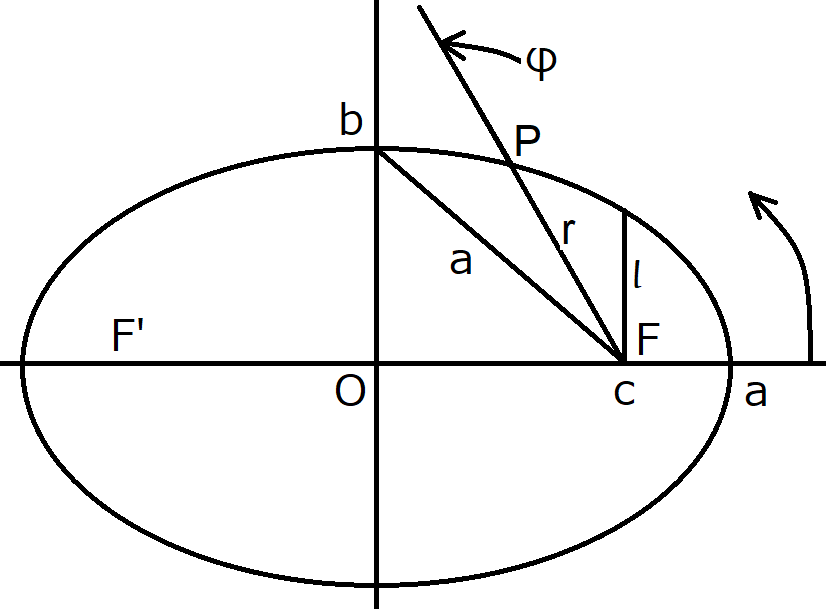

この図で考えます。
前回も書きましたが、ケプラーの第3法則は「惑星の公転周期の2乗は軌道の長半径の3乗に比例する」というものでした。惑星の公転周期をTとしましょう。軌道の長半径は図のa、短半径はbです。数学の公式によれば、楕円軌道の囲む面積Aは A=πab です。このとき公転周期TはAを面積速度で割れば求まり、
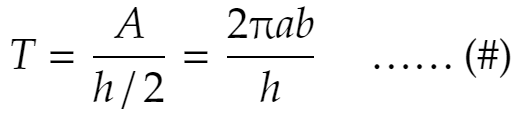
です。ケプラーの第3法則は

で、定数cは太陽系の全ての惑星に共通です。
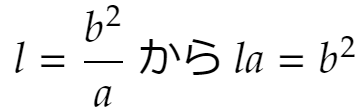
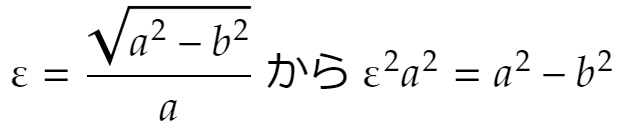
これより次を得ます。
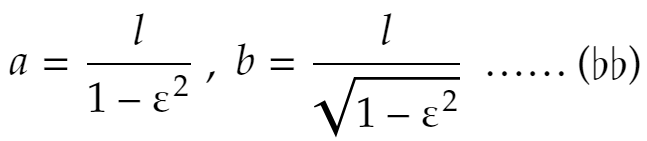
辺々かけて
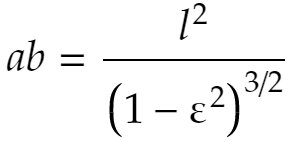
よって
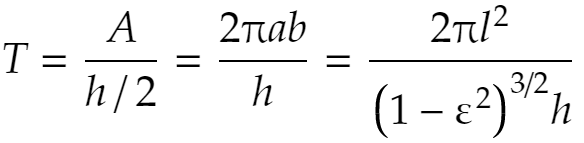
ゆえに(♭)は
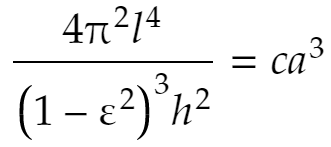
これに(♭♭)を用いて
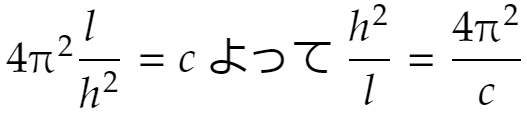
となり、これは惑星によりません。★★★に代入すれば
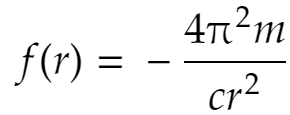
これは太陽の質量Mにも比例すると考えられるので、結局
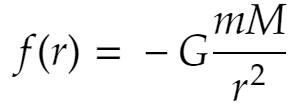
を得ます。
ニュートンのプリンキピアは読んだことがありませんが、こういう風に証明したんでしょうか……。ニュートンの証明は幾何学っぽい感じだったそうですが、内容的にはこうだったのかな……。しかしとにかく400年近く前のこと。凄いとしか言いようがありません。
今回の証明も『物理入門コース 力学』によっています。並行して『キーポイント力学』(吉田春夫1996岩波書店)も読んでいますが、こちらはこちらでまた面白いです。普通の力学のテキストとはかなり違います。目標を「惑星はなぜ楕円軌道を描くか」の理解とし、それに向けて丁寧に解説しています。
出かけるときには2冊持ち歩いて楽しんでいます。
どちらも2400円。安いと思います。最初のものは一体何ヶ月読んでいることか……。ちょっと映画でも見たりマンガでも読んだりすればアッという間に1000円、2000円。もちろん個人的な感覚ですが、こんな楽しいことがたったの2400円なのです。凄まじいコストパフォーマンスです。
