高校の数学ではあまり整数の問題は出てきません。まとまった時間、整数に関する体系的な説明はしないのです。他にやらなければならないことはたくさんあるから仕方ないんですが、面白いのに残念です……。暗号の理論に使われるなど応用面も広がりました。もっと扱ってもよいはず。そこで2回に分けてフェルマーの小定理まで案内しましょう。 整数論入門、第1回です。
7は素数です(素数とは:1と自分自身以外では割りきれない自然数のこと)。この7に対し、

を考えましょう。実はこれらの数はすべて7で割り切れます。実際、例えば

なので、分子の7は約分されずに残ってしまうからです。7は素数なので、分母の7より小さな数たちでは割り切れないのです。さて、a,bを整数とします。2項定理によれば

なのでした。先頭と一番最後の項だけを書き換えれば

ここで

はどれも7で割り切れるのだから、波線部分は7で割り切れます。だから、

を7で割った余りと

を7で割った余りは等しくなります。7が他の素数でも以上の議論は成り立ちますので、結局
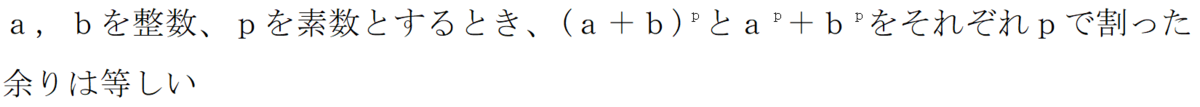
が証明されました。具体例で確認してみましょう。a=2、b=3、p=3としてみます。

を3で割ると、余りはどちらも2です。定理は成立しています。
ここからあとひとがんばりでフェルマーの小定理にたどり着きます。有名な

ではありません、小定理です。しかし「小」だからといって侮ってはいけません。頻繁に使われる、基本的な定理です。