a,bを整数、pを素数とするとき、
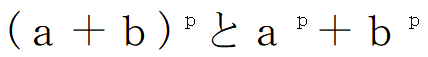
をそれぞれpで割った余りは等しい
が成立するのでした。ここでnを自然数とし、上の定理でa=1、b=1+1+………+1(n-1個の和)とおけば、
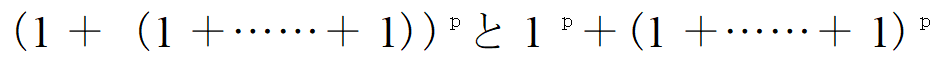
をpで割った余りは等しいことが分かります。つまり
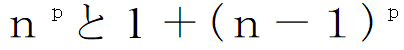
をpで割った余りは等しくなります。再び同じ式変形で
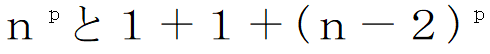
をpで割った余りは等しくなります。これを繰り返せば
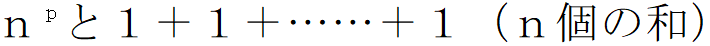
をpで割った余りは等しくなります。これで
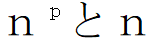
をpで割った余りが等しいことの証明ができました。まとめておきましょう。
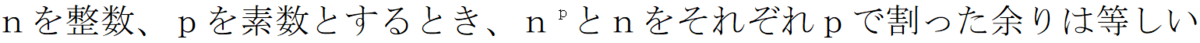
このとき
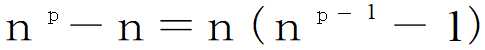
はpで割り切れます。
ここで(n,p)=1(n,pの最大公約数が1)のときは
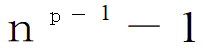
がpで割り切れます。以上でフェルマーの小定理
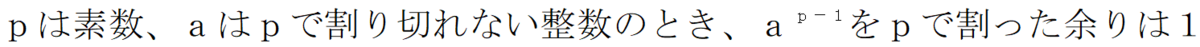
が得られました。証明の仕方は他にもあります。調べてみてください。前回書きましたが、この定理はあちこちに顔を出します。現代の暗号では数学を使います。整数論を使った暗号にはこの定理は必須です。がんばりましょう!