数Ⅱの恒等式の問題です。どう解きますか?
-----------------
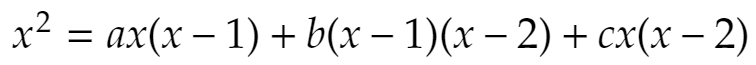
がxの恒等式になるよう、a,b,cを定めなさい。
-----------------
右辺を展開して係数を比較、とやってもいいですが、数値を代入する方法もあります。恒等式になるなら、x=0,1,2で等号が成立しなければなりません。x=0を代入すると0=2b、x=1を代入すると1=ーc、x=2を代入すると4=2aとなり、文字の値を求めるだけなら簡単です。a=2、b=0、c=-1です。しかし、ここでこれを答えにしてしまうとまずいのですね。このa,b,cは「x=0,1,2のときに最初の等式が成立する」ように定めた値だからです。つまりx=3のときは最初の等式が不成立になるかも知れないということです。だから、a=2、b=0、c=-1のときに最初の式が本当に恒等式になるか、確認しなければならないわけです。具体的には右辺を展開して左辺に一致することを見ればよいでしょう。念押しすると、a=2、b=0、c=-1は恒等式であるための必要条件なのです。実際にこのとき恒等式になることは別途、確認しなければならないということです。
しかし、次の定理を証明しておけばこの確認は不要になります。
「n次以下の整式をf(x)、g(x)とするとき、n+1個のxの異なる値でf(x)=g(x)が成立すればf(x)=g(x)は恒等式である」
何次でも同じですから、2次以下の整式で考えましょう。f(x)=g(x)の右辺を左辺へ移項してf(x)-g(x)を改めてf(x)とおき、次を示せばよいですね。
「2次以下の整式をf(x)とするとき、3個のxの異なる値でf(x)=0が成立すればf(x)=0は恒等式である」
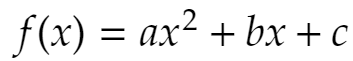
であるとしておきます。例えばf(1)=0、f(2)=0、f(3)=0だとしましょう。f(1)=0からf(x)はx-1で割り切れ、f(2)=0からf(x)はx-2で割り切れ、f(3)=0からf(x)はx-3で割り切れます。よってf(x)=(x-1)(x-2)(x-3)Q(x)となるはずです(Q(x)はxの整式)。ここでf(x)は2次以下ですから、Q(x)=0(整式として0)でなければなりません。よってf(x)=0は恒等式です。
この定理を使えば、最初の問題はx=1,2,3で等号成立なのですからそれだけで恒等式と言えます。
授業をするならこのくらいの話はしたい気がします。話のもって行き方によっては代数学の基本定理に触れてもいいですし、面白そうです。f(x)がn次以下の整式なら、代数学の基本定理によればf(x)=0の異なる解はn個以下なので、異なるn+1個のxに対してf(x)=0となるためにはf(x)は整式として0でなければなりません、とやればよいのですね。
代数学の基本定理とは:
「n次の代数方程式はn個の解を複素数の範囲に持つ」というものでした(ただしk重解はk個の解とカウント)。