前回の続きです。後で説明しますが、３枚の写真から基礎行列Fを求めるとき、（方法によりますが）３元（変数が３個）４次の連立方程式を解く必要があります。Pythonに何かないかなと思って探していたらSymPyというライブラリがありました。試してみたので紹介しておきましょう。見るとすぐ分かりますが、コードでは例えば「ｘ＋3ｙ＝2」は「ｘ＋3ｙ－2」と表現しますので注意。
from sympy import *
import sys
x, y, z = symbols('x y z')
init_printing()
ans = solve([x * x + y * y -10, -x + y - 2], [x, y])
print(ans)
ans = solve([-x + y -6 * z - 10, 2 * x + y - z - 1, x + y + z - 5], [x, y, z])
print(ans)
sys.exit()連立方程式は２つ、用意しました。
１つめは
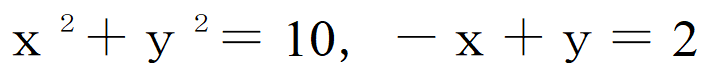、平面で円と直線の交点を求めています。２つ目は ーｘ＋ｙ－６ｚ＝１０，２ｘ＋ｙ－ｚ＝１，ｘ＋ｙ＋ｚ＝５。これは空間で３枚の平面の交点を求めています。結果は次の通り。
ーーーーーーーーーーーー
[(-3, -1), (1, 3)]
{x: -38/11, y: 90/11, z: 3/11}
ーーーーーーーーーーーー
おお、これはすごい！！ しっかり求まっています。SymPy、使わせてもらいます。
実際に必要な連立方程式はいずれ書きますが、解くとカメラの内部パラメータの行列が得られます。カメラ固有の値を成分に持つ3行3列の行列です。これによってカメラ行列を求めることができ、写真に写っている点が空間内のどこにあるのか計算できるようになるのです。今は「ほう、そんなもんか」でよいと思います。
きちんと理屈をたどれば、なぜ写真から立体を再現できるのか理解できます。エキサイティングです！ そして、実験をしてみて理論通りの結果が出るのもエキサイティングです！ 面白くて勉強がやめられません。
