後で使うので、固有値、固有ベクトル、連立方程式の非自明解を求めます。例によってPythonです。
#========================================================
#固有値、固有ベクトル、非自明解
#
import sys
import numpy as np
A = np.array([[3, 1, 2], [3, 2, 1], [0, 1, -1]])
print('rank = ', np.linalg.matrix_rank(A))
B, C = np.linalg.eig(A) #固有値、固有ベクトルを求める
print('A = \n', A)
print('固有値 = \n', B)
#Cの列ベクトルが固有ベクトルなので、転置して取り出す
print('固有ベクトル = \n', C.T)
print('A * 固有ベクトル = ')
for i in range(0, 3):
print(np.dot(A, C.T[i])) #A*固有ベクトルを計算
sys.exit()実行結果は以下の通りです。
rank = 2
A =
[[ 3 1 2]
[ 3 2 1]
[ 0 1 -1]]
固有値 =
[ 4.64575131e+00 1.28359373e-16 -6.45751311e-01]
固有ベクトル =
[[-0.6295454 -0.76505532 -0.13550992]
[ 0.57735027 -0.57735027 -0.57735027]
[-0.51994159 0.28523152 0.8051731 ]]
A * 固有ベクトル =
[-2.92471137 -3.55425677 -0.6295454 ]
[-6.66133815e-16 -8.88178420e-16 -2.22044605e-16]
[ 0.33575296 -0.18418863 -0.51994159]
行列Aのランクは2、得られた固有値3個うちの2個目が0です。連立方程式 AX=0 は、Aが3次の行列なのでランクが3なら非自明解を持たず、ランクが2以下なら持つはずです。固有値0に対応する固有ベクトルは、固有ベクトルのリストの2本目の [0.57735027, …………] です。実際にこれをAにかけてみると0ベクトルが得られました。
Aが正方行列でなくても、AX=0の非自明解は求められます。
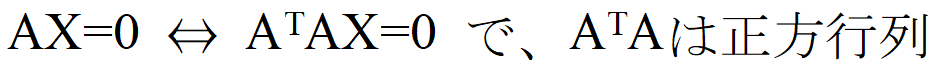
なのですから、これを利用すればよいのです。あるいは、Aの特異値分解を利用する方法もありますが、これはまた後ほど。