新・写真から立体を再現（7）Pythonのコードを載せます

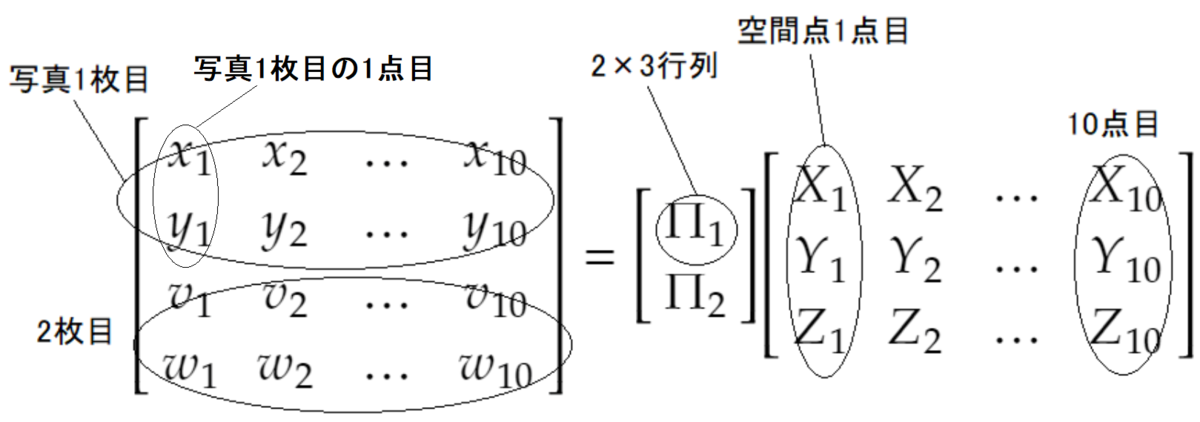
　前回の続きです。2枚の写真を再掲。


　とりあえず立体を再現するためのコードを載せておきます。2枚の写真は「a.jpg」、「b.jpg」としてありますが、変えられます。1枚目の写真のマジックの位置を25点、マウスでクリックします。それが終わったら対応順を間違えないように2枚目で25回クリック。拾う点の数はコードのNの値で指定。合計50回クリックしたらエスケープキーを押せば必要な計算がなされ、散布図が描かれます。短いコードですし、大変なことはしていないので分かりやすいかと。
　近似なしでいろいろ考えてきましたが、（程度もありますが）前回のように「大体の計算でよい」ということならラクになります。今後はそういった方面でも考えてみたいです。

import sys
import numpy as np
import cv2
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#-----------------------------------
#初期値
#
i = 0
N = 25 #写真上でN点選ぶ(写真2枚で2N点)
#-----------------------------------
ptlist = np.zeros([2, N, 2]) #写真2枚、N点ずつのxy座標
ptList = np.zeros([4, N]) #ptlist を行列で
#-----------------------------------
#画像上の座標(p, q)を(x, y)に直す
#画像中央を原点、右へ進むと＋、上に進むと＋
#（画像上の座標は左上が原点）
#
def convCoor(w, h, p, q):
    x = -w/2 + p
    y = h/2 - q
    return x, y
#-----------------------------------
#コールバック関数 #12
#マウスイベントが起こるとここへ来る
#マウスで拾った画像上の座標は写真の中心が原点
#
def getClickPt(event, x, y, flags, param):
    global i
    if event == cv2.EVENT_LBUTTONDOWN:
        if i < N:
            v, w = convCoor(w1, h1, x, y)
            ptlist[0, i] = [v, w]
        elif N <= i < 2*N:
            v, w = convCoor(w2, h2, x, y)
            ptlist[1, i-N] = [v, w]
        i = i + 1
        print([v, w])
    return
#-----------------------------------
# main routine
#-----------------------------------
img = cv2.imread('a.jpg')
h1 = img.shape[0]
w1 = img.shape[1]
img2 = cv2.imread('b.jpg')
h2 = img2.shape[0]
w2 = img2.shape[1]
#画像のウインドウに名前をつけ、コールバック関数をセット
cv2.imshow('image',img)
cv2.namedWindow('image')
cv2.setMouseCallback('image',getClickPt)
cv2.moveWindow('image', 100, 50)
cv2.imshow('image2',img2)
cv2.namedWindow('image2')
cv2.setMouseCallback('image2',getClickPt)
cv2.moveWindow('image2', 800, 50)
#-----------------------------------
while(1):
    #ESCキーでブレーク
    if cv2.waitKey(20) & 0xFF == 27: #エスケープキーで抜ける
        break
#-----------------------------------
ptList[0] = ptlist[0].T[0] #取得した写真上の点の座標を行列の形にまとめる
ptList[1] = ptlist[0].T[1]
ptList[2] = ptlist[1].T[0]
ptList[3] = ptlist[1].T[1]
print('ptList\n', ptList)
print('rank(ptList) =  ', np.linalg.matrix_rank(ptList), '\n')
for i in range(4):
    ptList[i] = ptList[i] - np.mean(ptList[i]) #平均を引く
U, S, VT = np.linalg.svd(ptList) #特異値分解
print('U = \n', U)
print('S = \n', np.diag(S))
print('VT = \n', VT)
X = VT[0:3, 0:N] #VTから空間の点の座標を取り出す
print('X = \n', X)
fig = plt.figure()
#add_subplotの最初の3つの引数は通常なら「1,1,1」でよい
ax = fig.add_subplot(1,1,1, projection='3d')
x = X[0]
y = X[1]
z = X[2]
ax.scatter(x, y, z) #散布図を描画
plt.show()
sys.exit()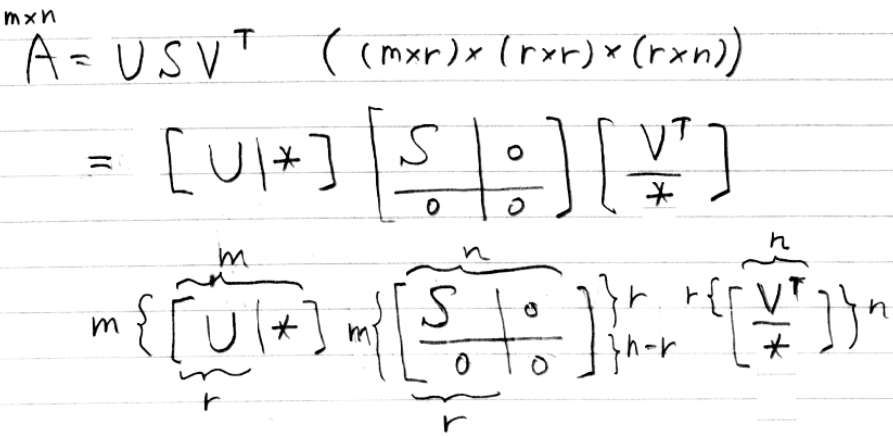

Numpyの特異値分解では、上の式の最後の形が得られます。コードの「#VTから空間の点の座標を取り出す」のところでは、得られる行列VTから空間点、つまり最初の3行を取り出しています。「#平均を引く」のところでは、写真上の点の座標の平均が0となるようにしています。こうすることによって前回の記事の次の式が使えるようになります。