前、「対数を使って2の1000乗の桁数を求められるか」というタイトルで記事を書きました。
www.omoshiro-suugaku.com
例えばこんな問題を考えます。
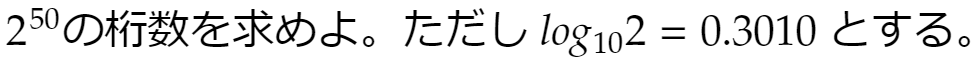
常用対数をとると
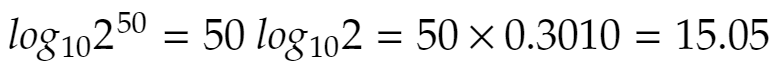
ゆえに
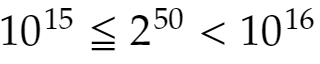
よって16桁ということになります。上の記事で説明したように、対数の値を近似値で扱うと桁数に狂いが出る可能性があります。そこで、どんなときに安全に桁数を計算できるのか、それを判断するためのある不等式をすでに示してあります。今回は実際にパソコンで、累乗の指数がどんな値のときにズレが生じるのか、実験してみます。
そもそも、どんなときに近似値を使ったときと真の値を使ったときとでズレるのか? 2の累乗の指数をmとしましょう。桁数の計算の仕方から、
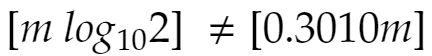 ……★
……★
であるとき、値が狂うのです([ ]はガウス記号)。もともと左辺で桁を計算したいのに、対数の真の値を使うわけにはいかないから0.3010で代用します。その結果が桁数のズレにつながります。そこで、m=1,2,3,……,1000,1001,……,1999として、mがどんな値のときに★が成立するのか(つまり値が狂うのか)単純に調べてみます。
#---------------------------------
import math
for m in range(2000):
if int(m*math.log10(2)) != int(0.3010*m):
print(m) #, m*math.log10(2), m*0.3010)
#---------------------------------pythonで調べました。結果は次の通り。
196
299
392
495
588
598
681
691
784
794
877
887
897
980
990
1073
1083
1093
1166
1176
1186
1196
1269
1279
1289
1299
1362
1372
1382
1392
1465
1475
1485
1495
1558
1568
1578
1588
1598
1651
1661
1671
1681
1691
1754
1764
1774
1784
1794
1847
1857
1867
1877
1887
1897
1950
1960
1970
1980
1990
実際、例えば196乗のときは
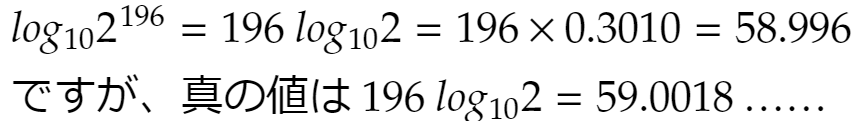
ですから、桁数に狂いが生じます。
500乗とかでズレが起こると、場合によっては試験で使ってしまう先生がいたりして、トラブルになるかも知れません。でも上のリストには試験で使われそうな半端でない数はありません。多分あまり気にせず問題を作ってもまあ大丈夫、ということになりそうです。ご安心ください!