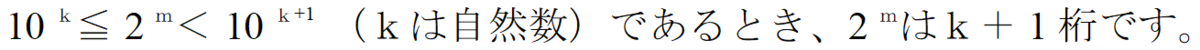
常用対数をとると
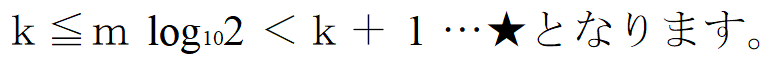
高校では対数のところで出てくる問題です。
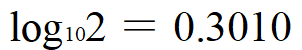
として答えなさい、などと但し書きがあります。これは近似値ですからもちろん真の値とは異なり、mによっては桁数に誤りが出る可能性があります。たいていはm=30とかm=50程度なので問題ないのですが、ではmがどの程度になると危ないのでしょうか。mがある程度以上になると

の差が大きくなるわけです。
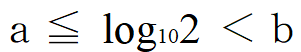
であるとします。各辺をm倍して
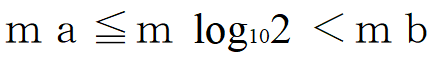
を得ますから、さっきの★を考えて k≦maかつmb≦k+1となる自然数kがあればk+1桁に確定、となります。つまりmb-1≦k≦ma、すなわち mb ≦ k+1 ≦ ma+1 が成立すればk+1桁となります。これは十分条件であって、不成立だから桁数を求められない、と断言はできません。念のため。
さて、
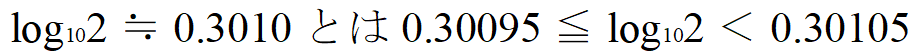
ということですから、a=0.30095、b=0.30105とおきましょう。
0.30105m ≦ k+1 ≦ 0.30095m+1 であればk+1桁に確定です。あとはmに具体的な値を入れて、その式を満たすkがあるかどうか確認すればよいのです。例えばm=200とすると 60.21 ≦ k+1 ≦ 61.19で、kは定まります。だからこのときは桁数は正確に求まります。しかしm=1000とすると 301.05 ≦ k+1 ≦ 301.95 となってkがありません。つまり1000乗の時は正しい桁が計算できるかどうか不明、ということになります。
以上、ある程度結果を出したのでまとめておきます。
追記:
2020年5月27日(水) 代入のミス、計算ミスを訂正しました。