いくつかのテキストで、複数枚の写真だけからそれに写っている立体を再現する手順の一部に射影幾何の知識を用いています。ぼくはこれまで、射影幾何を体系的に勉強したことがありません。大学でも、少なくとも微積分並みに教えていたわけではないと思います。射影幾何を避ける方法もあり、今回「新・写真から立体を再現する」シリーズではこちらを使うつもりでした。が、この機会に必要な勉強をしておくのもよいかと考えて取り組んでみることに。少しずつ書きます。
------------------
定理をひとつ、紹介しましょう。
原点中心、半径rの円を考えます。式は
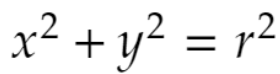
なのでした。この円の外の点Pから円に接線を2本引きます。接点をA、Bとしましょう。直線ABは点Pの極線、Pは直線ABの極と呼ばれます。極線AB上に点Qを取り、Qから再び円に接線を2本引き、接点をC、Dとします。直線CDは点Qの極線です。実はこのとき極線CD上にもとの点Pが乗っています。
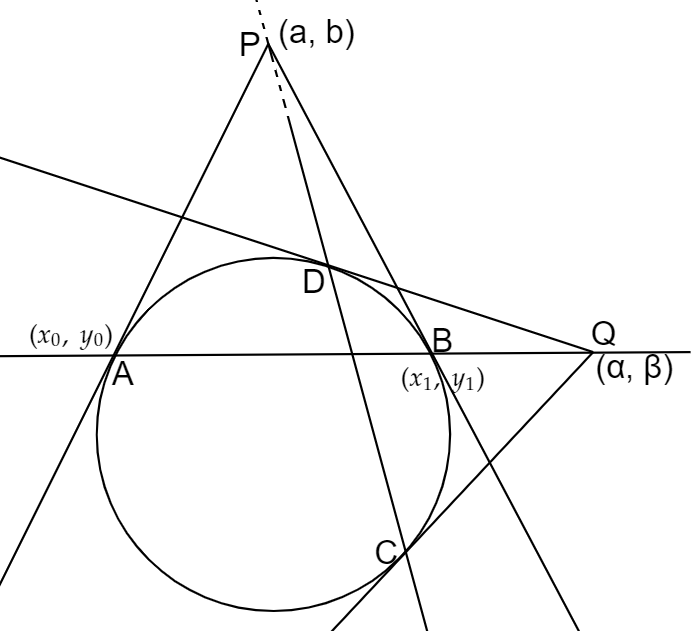
不思議な事実と言えます。数学Ⅱの知識を用いて証明してみます。
まず、点Pの極線は
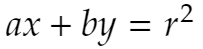 ……①
……①
であることを示します。①が2点A、Bを通ることを示せばよいですね。
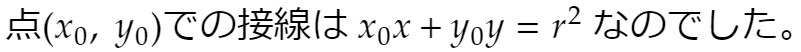
この直線が(a, b)を通るので、
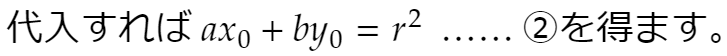
この式②は、①が点Aを通ることを示しています。同様に①は点Bも通ります。従って①は点Pの極線の方程式です。
次に、点Pの極線AB上に点Qを取ります。Q(α, β)とすると、極線の式①に代入して
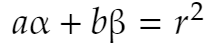 ……③
……③
が分かります。ところでQ(α, β)の極線は①と同じことで
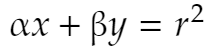
ですが、さっきの③はこの極線上に点(a, b)が乗っていることを示しています。以上です。
------------------
面白そうなんですが、テキストは少ないと思います。今回の内容は『射影幾何』( 津田丈夫1981共立出版数学ワンポイント双書)によります。例によって説明などは自分で分かりやすいように書き換えてしまっています。この定理は円錐曲線が持つ基本的な性質だそうで、射影幾何を発展させたポンスレはこれを利用して双対(そうつい)の原理を発見したそうです。勉強します……。