数列{}の階差数列{
}からもとの数列{
}を求めます。公式がありました。
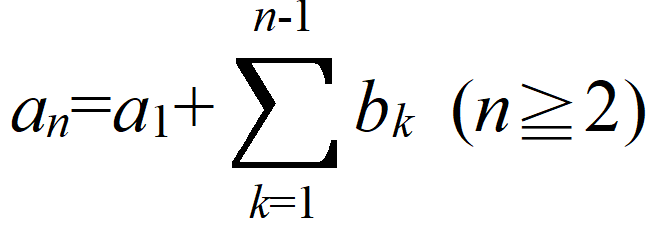
というものです。これを用いれば
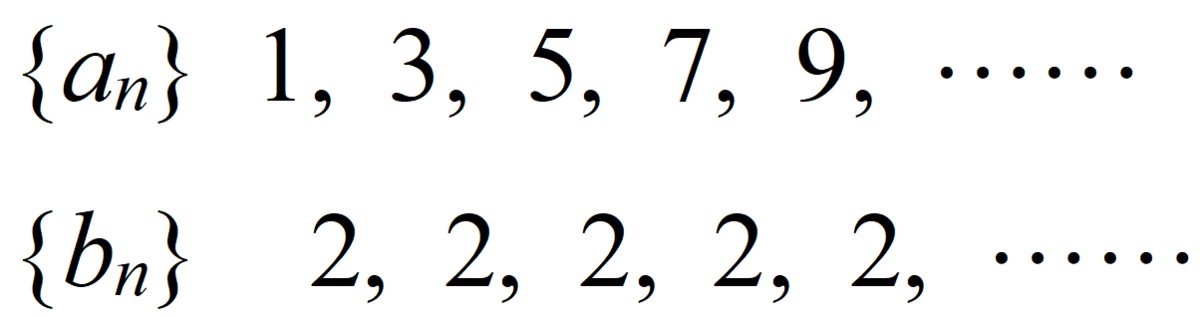
のとき、もとの数列は以下のように求められます(n≧2)。
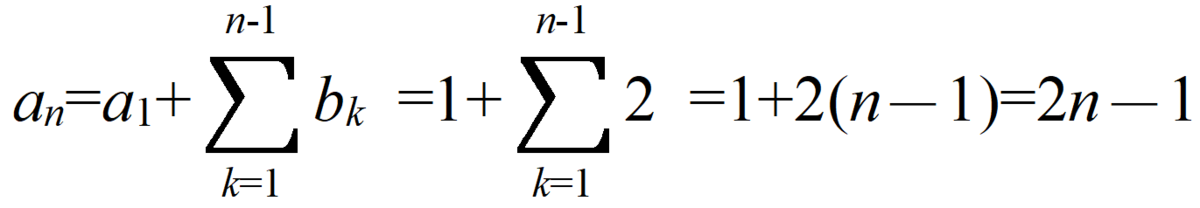
これはn=1でも成立します。ところで……n=1では成立しない例はあるのでしょうか? 教科書などでは成立する問題ばかりですが……。
実はあるのです!!
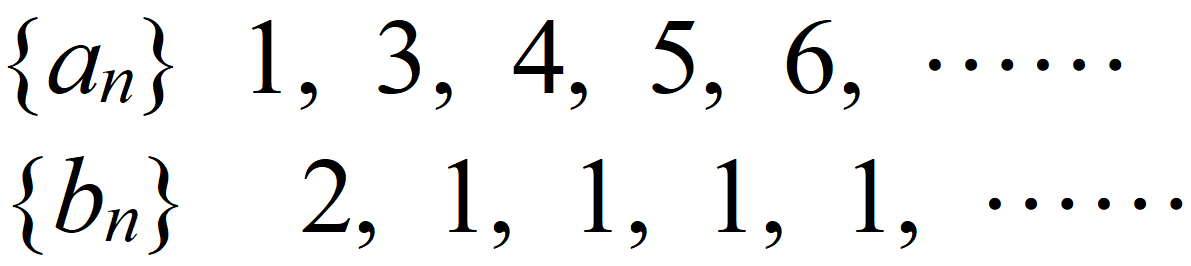
など、どうですか?

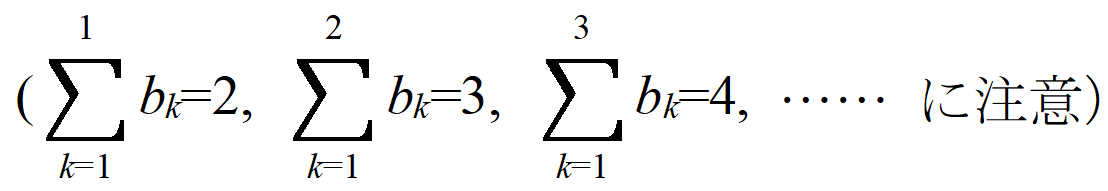
となって、これはn=1では不成立です。最初の公式はその導き方からしてそもそもn=1のときには使えませんが、成立の場合もたくさんあるのですね。しかし不成立の例も今回示したようにあり、こうなるともう毎回「成立するのか? しないのか?」確認せざるを得なくなります。仕方ありません。